题目内容
已知x = 4是函数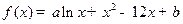 的一个极值点,(
的一个极值点,(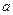 ,b∈R).
,b∈R).
(Ⅰ)求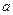 的值;
的值;
(Ⅱ)求函数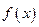 的单调区间;
的单调区间;
(Ⅲ)若函数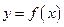 有3个不同的零点,求
有3个不同的零点,求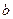 的取值范围.
的取值范围.
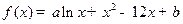 的一个极值点,(
的一个极值点,(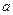 ,b∈R).
,b∈R).(Ⅰ)求
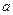 的值;
的值; (Ⅱ)求函数
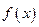 的单调区间;
的单调区间;(Ⅲ)若函数
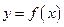 有3个不同的零点,求
有3个不同的零点,求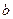 的取值范围.
的取值范围.(Ⅰ)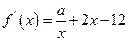 , (x>0)…………………2’
, (x>0)…………………2’
由已知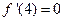 得,
得, 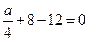 , 解得
, 解得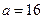 . ……4’
. ……4’
(Ⅱ)由(Ⅰ)知,
 ,
,
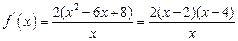 .
.
当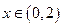 时,
时,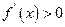 ;当
;当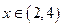 时,
时,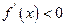 ;
;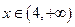 时,
时,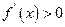 .
.
所以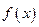 的单调增区间是
的单调增区间是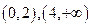 ;
;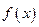 的单调减区间是
的单调减区间是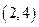 .…………8’
.…………8’
(Ⅲ)由(Ⅱ)知,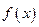 在
在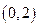 内单调递增,在
内单调递增,在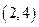 内单调递减,在
内单调递减,在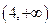 上单调递增,
上单调递增,
且当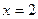 或
或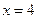 时,
时,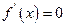 .
.
所以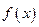 的极大值为
的极大值为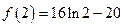 +b,极小值为
+b,极小值为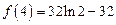 +b.…………10’
+b.…………10’
又因为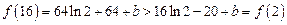 ,
,
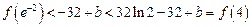 .
.
当且仅当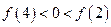 ,
,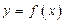 有三个零点.…………12’
有三个零点.…………12’
所以,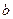 的取值范围为
的取值范围为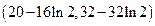 . ………………………14’
. ………………………14’
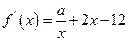 , (x>0)…………………2’
, (x>0)…………………2’由已知
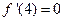 得,
得, 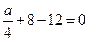 , 解得
, 解得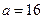 . ……4’
. ……4’(Ⅱ)由(Ⅰ)知,
 ,
,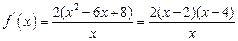 .
.当
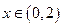 时,
时,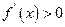 ;当
;当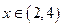 时,
时,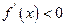 ;
;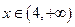 时,
时,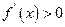 .
.所以
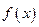 的单调增区间是
的单调增区间是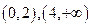 ;
;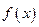 的单调减区间是
的单调减区间是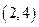 .…………8’
.…………8’(Ⅲ)由(Ⅱ)知,
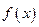 在
在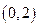 内单调递增,在
内单调递增,在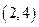 内单调递减,在
内单调递减,在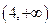 上单调递增,
上单调递增,且当
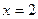 或
或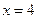 时,
时,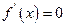 .
.所以
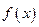 的极大值为
的极大值为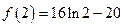 +b,极小值为
+b,极小值为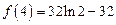 +b.…………10’
+b.…………10’又因为
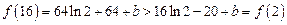 ,
,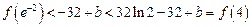 .
.当且仅当
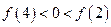 ,
,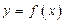 有三个零点.…………12’
有三个零点.…………12’所以,
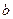 的取值范围为
的取值范围为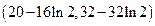 . ………………………14’
. ………………………14’略

练习册系列答案
相关题目
 = ▲ .
= ▲ .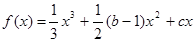 (b、c为常数).
(b、c为常数).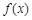 在
在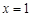 和
和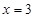 处取得极值,试求b,c的值;
处取得极值,试求b,c的值;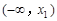 、
、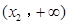 上单调递增,且在
上单调递增,且在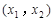 上单调递减,又满足
上单调递减,又满足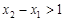 ,求证:
,求证: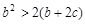 .
.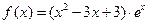 定义域为
定义域为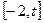 (
(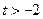 ),设
),设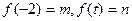 .
.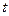 的取值范围,使得函数
的取值范围,使得函数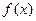 在
在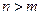 ;
;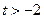 ,总存在
,总存在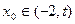 ,满足
,满足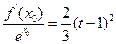 ,并确定这样的
,并确定这样的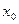 的个数.
的个数.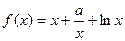 ,
,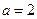 时,求函数
时,求函数 的单调增区间;
的单调增区间; 时,f
时,f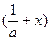 >f
>f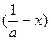 ;
;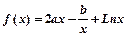
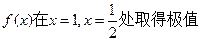 ,
, 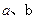 的值;
的值;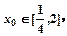 使得不等式
使得不等式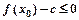 成立,求
成立,求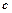 的最小值;
的最小值;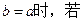
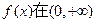 上是单调函数,求
上是单调函数,求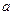 的取值范围。
的取值范围。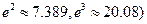
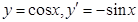 ; ②若
; ②若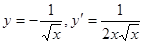 ;
;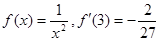 ; ④若
; ④若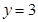 ,则
,则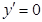 .正确个数是( )
.正确个数是( )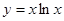 的导数为________
的导数为________