Question

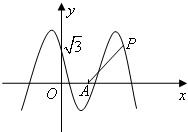
如图，函数y=2cos(ωx+θ)(x∈R，0≤θ≤

π

2

)的图象与y轴交于点(0，

3

)，且在该点处切线的斜率为-2．
（1）求θ和ω的值；
（2）已知点A(

π

2

，0)，点P是该函数图象上一点，点Q（x₀，y₀）是PA的中点，当y0=

3

2

，x0∈[

π

2

，π]时，求x₀的值．

Answer 1

（1）将x=0，y=

3

代入函数y=2cos（ωx+θ）得cosθ=

3

2

，
因为0≤θ≤

π

2

，所以θ=

π

6

．
又因为y'=-2ωsin（ωx+θ），y'|_x=0=-2，θ=

π

6

，所以ω=2，
因此y=2cos(2x+

π

6

)．
（2）因为点A(

π

2

，0)，Q（x₀，y₀）是PA的中点，y0=

3

2

，
所以点P的坐标为(2x0-

π

2

，

3

)．
又因为点P在y=2cos(2x+

π

6

)的图象上，所以cos(4x0-

5π

6

)=

3

2

．
因为

π

2

≤x0≤π，所以

7π

6

≤4x0-

5π

6

≤

19π

6

，
从而得4x0-

5π

6

=

11π

6

或4x0-

5π

6

=

13π

6

．
即x0=

2π

3

或x0=

3π

4

．