题目内容
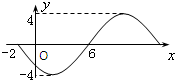
已知函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,-
<φ<
),其部分图象如图所示.
(I)求f(x)的解析式;
(II)求函数g(x)=f(x+
)•f(x-
)在区间[0,
]上的最大值及相应的x值.

| π |
| 2 |
| π |
| 2 |
(I)求f(x)的解析式;
(II)求函数g(x)=f(x+
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |

(I)由图可知,A=1(1分)
=
,所以T=2π(2分)
所以ω=1(3分)
又f(
)=sin(
+ϕ)=1,且-
<φ<
所以ϕ=
(5分)
所以f(x)=sin(x+
).(6分)
(II)由(I)f(x)=sin(x+
),
所以g(x)=f(x+
)•f(x-
)=sin(x+
+
)•sin(x-
+
)=sin(x+
)sinx(8分)
=cosx•sinx(9分)
=
sin2x(10分)
因为x∈[0,
],所以2x∈[0,π],sin2x∈[0,1]
故:
sin2x∈[0,
],
当x=
时,g(x)取得最大值
.(13分)
| T |
| 4 |
| π |
| 2 |
所以ω=1(3分)
又f(
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
所以ϕ=
| π |
| 4 |
所以f(x)=sin(x+
| π |
| 4 |
(II)由(I)f(x)=sin(x+
| π |
| 4 |
所以g(x)=f(x+
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
=cosx•sinx(9分)
=
| 1 |
| 2 |
因为x∈[0,
| π |
| 2 |
故:
| 1 |
| 2 |
| 1 |
| 2 |
当x=
| π |
| 4 |
| 1 |
| 2 |

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目

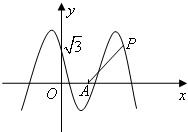
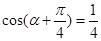 ,则
,则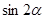 的值为 ( ).
的值为 ( ).