Question

【题目】在直角坐标平面上，称横、纵坐标都是有理数的点为有理点．求满足如下条件的最小正整数：每一个圆周上含有个有理点的圆，它的圆周上一定含有无穷多个有理点．

Answer 1

【答案】的最小值为3

【解析】

首先证明：若一个圆的圆周含有3个有理点，则该圆周上一定含有无穷多个有理点．

设平面上的圆周上含有2个有理点（），圆心．

由于线段的垂直平分线过圆心，则

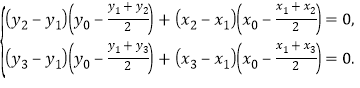
由于（）都是有理数，因此，上述关于的二元一次方程组的解都是有理数，即是有理点．设有理点的坐标为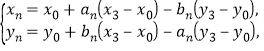

其中，（）．

则

．

故点（）都在的圆周上，即的圆周上有无穷多个有理点．其次，构造一个圆周上只含有两个有理点的实例．．容易验证，都在圆周上．

若圆周上还有不同于的有理点，

则，即．

因为左端为有理数，为无理数，所以，．进而．

故．这与不同于的假定矛盾．综上所述，的最小值为3．