题目内容
【题目】已知中心在原点O，焦点在x轴上的椭圆的一个顶点为B（0，1），B到焦点的距离为2． 
（1）求椭圆的标准方程；
（2）设P，Q是椭圆上异于点B的任意两点，且BP⊥BQ，线段PQ的中垂线l与x轴的交点为（x0 ， 0），求x0的取值范围．
【答案】
（1）解：∵中心在原点O，焦点在x轴上的椭圆的一个顶点为B（0，1），B到焦点的距离为2．
∴由条件：b=1，a=2，
∴椭圆的标准方程为： 
=1
（2）解：①当直线PQ斜率k=0时，线段PQ的中垂线l在x轴上的截距为0；
②设PQ：y=kx+m，（k≠0），
则： 
﹣4=0，
设P（x1，y1），Q（x2，y2），
则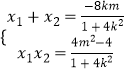 
，
∵BP⊥BQ，∴ 
，
∴（1+k2）x1x2+k（m﹣1）（x1+x2）+（m﹣1）2=0（1+k2） 
=0
∴5m2﹣2m﹣3=0m=﹣ 
或m=1（舍去），
∴PQ为：y=kx﹣ ，
∴xM= 
，yM= 
，
∴线段PQ的中垂线l为：y+ 
，
∴在x轴上截距x0= 
，
∴|x0|= 
，
∴﹣ 
且x0≠0，
综合①②得：线段PQ的中垂线l在x轴上的截距的取值范围是 
【解析】（1）由条件b=1，a=2，由此能求出椭圆的标准方程．（2）当直线PQ斜率k=0时，线段PQ的中垂线l在x轴上的截距为0；当k≠0时，设PQ：y=kx+m，取椭圆联立得（1+4k2）x2+8kmx+4m2﹣4=0，由此利用韦达定理、向量垂直、中垂线性质，结合已知条件能求出线段PQ的中垂线l在x轴上的截距的取值范围．
练习册系列答案
快乐5加2金卷系列答案
相关题目
