[题目]设A1 . A2 . -.An为集合S={1.2.-.n}的n个不同子集.为了表示这些子集.作n行n列的数阵.规定第i行第j列的数为: ．则下列说法中.错误的是( ) A.数阵中第一列的数全是0当且仅当A1=B.数阵中第n列的数全是1当且仅当An=SC.数阵中第j行的数字和表明集合Aj含有几个元素D.数阵中所有的n2个数字之和不超过n 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】设A1 ， A2 ， …，An（n≥4）为集合S={1，2，…，n}的n个不同子集，为了表示这些子集，作n行n列的数阵，规定第i行第j列的数为：．则下列说法中，错误的是（）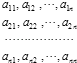

A.数阵中第一列的数全是0当且仅当A1=
B.数阵中第n列的数全是1当且仅当An=S
C.数阵中第j行的数字和表明集合Aj含有几个元素
D.数阵中所有的n2个数字之和不超过n2﹣n+1

【答案】C
【解析】解：数阵中第一列的数全是0，当且仅当1A1 ， 2A1 ， …，nA1 ， ∴A正确；
数阵中第n列的数全是1当且仅当1∈An ， 2∈An ， …，n∈An ， ∴B正确；
当A1 ， A2 ， …，An中一个为S本身，其余n﹣1个子集为S互不相同的n﹣1元子集时，数阵中所有的n2个数字之和最大，且为n+（n﹣1）2=n2﹣n+1，∴D正确；
数阵中第j行的数字和表明元素j属于几个子集，∴C错误．
故选：C．

练习册系列答案

相关题目

【题目】设关于x的一元二次方程x2+2ax+b2=0．
（1）若a是从0，1，2，3四个数中任取的一个数，b是从0，1，2三个数中任取的一个数，求上述方程有实根的概率．
（2）若a是从区间[0，3]任取的一个数，b是从区间[0，2]任取的一个数，求上述方程有实根的概率．

【题目】在△ABC中，内角A，B，C的对边分别为a，b，c．已知acosB﹣c= ．
（1）求角A的大小；
（2）若b﹣c= ，a=3+ ，求BC边上的高．

【题目】数列{an}中，已知a1= ，an+1= ．
（1）证明：an＜an+1＜；
（2）证明：当n≥2时，（）＜2．

【题目】如图，在多面体EF﹣ABCD中，ABCD，ABEF均为直角梯形，，DCEF为平行四边形，平面DCEF⊥平面ABCD．

（1）求证：DF⊥平面ABCD；
（2）若△ABD是等边三角形，且BF与平面DCEF所成角的正切值为，求二面角A﹣BF﹣C的平面角的余弦值．

【题目】已知中心在原点O，焦点在x轴上的椭圆的一个顶点为B（0，1），B到焦点的距离为2．

（1）求椭圆的标准方程；
（2）设P，Q是椭圆上异于点B的任意两点，且BP⊥BQ，线段PQ的中垂线l与x轴的交点为（x0 ， 0），求x0的取值范围．

【题目】《九章算术》是我国古代数学名著，它在几何学中的研究比西方早1千多年．在《九章算术》中，将底面为直角三角形，且侧棱垂直于底面的三棱柱称为堑堵，阳马指底面为矩形，一侧棱垂直于底面的四棱锥，鳖臑指四个面均为直角三角形的四面体．如图，在堑堵ABC﹣A1B1C1中，AC⊥BC．
（Ⅰ）求证：四棱锥B﹣A1ACC1为阳马；并判断四面体B﹣A1CC1是否为鳖臑，若是，请写出各个面的直角（只要求写出结论）．
（Ⅱ）若A1A=AB=2，当阳马B﹣A1ACC1体积最大时，求二面角C﹣A1B﹣C1的余弦值．

【题目】若实数x，y满足：x2+y2﹣2x﹣2y=0，则x+y的取值范围是（）
A.[﹣4，0]
B.[2﹣2 ，2+2 ]
C.[0，4]
D.[﹣2﹣2 ，﹣2+2 ]

【题目】已知椭圆经过点，且离心率为．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设A，B是椭圆C的左，右顶点，P为椭圆上异于A，B的一点，以原点O为端点分别作与直线AP和BP平行的射线，交椭圆C于M，N两点，求证：△OMN的面积为定值．

试题分类