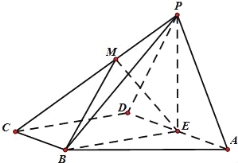
题目内容
【题目】如图，正三棱柱
各条棱的长度均相等，
为
的中点，
分别是线段
和线段
的动点（含端点），且满足
，当运动时，下列结论中不正确的是
A. 在
内总存在与平面
平行的线段
B. 平面
平面
C. 三棱锥
的体积为定值
D. 可能为直角三角形
【答案】D
【解析】
A项用平行于平面ABC的平面与平面MDN相交，则交线与平面ABC平行；
B项利用线面垂直的判定定理；
C项三棱锥
与三棱锥
体积相等，三棱锥的底面积是定值，高也是定值，则体积是定值;
D项用反证法说明三角形DMN不可能是直角三角形.
A项，用平行于平面ABC的平面截平面MND，则交线平行于平面ABC，故正确；
B项，如图：
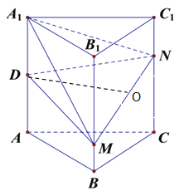
当M、N分别在BB1、CC1上运动时,若满足BM=CN,则线段MN必过正方形BCC1B1的中心O,由DO垂直于平面BCC1B1可得平面
平面
，故正确；
C项,当M、N分别在BB1、CC1上运动时,△A1DM的面积不变,N到平面A1DM的距离不变,所以棱锥N-A1DM的体积不变,即三棱锥A1-DMN的体积为定值,故正确；
D项,若△DMN为直角三角形,则必是以∠MDN为直角的直角三角形,但MN的最大值为BC1,而此时DM,DN的长大于BB1,所以△DMN不可能为直角三角形,故错误.
故选D
练习册系列答案
相关题目
