题目内容
【题目】甲、乙、丙三人准备报考某大学,假设甲考上的概率为 ![]() ,甲,丙两都考不上的概率为
,甲,丙两都考不上的概率为 ![]() ,乙,丙两都考上的概率为
,乙,丙两都考上的概率为 ![]() ,且三人能否考上相互独立.
,且三人能否考上相互独立.
(1)求乙、丙两人各自考上的概率;
(2)设X表示甲、乙、丙三人中考上的人数与没考上的人数之差的绝对值,求X的分布列与数学期望.
【答案】
(1)解:设A表示“甲考上”,B表示“乙考上”,C表示“丙考上”,
则P(A)= ![]() ,且
,且 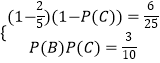 ,
,
解得P(C)= ![]() ,P(B)=
,P(B)= ![]() .
.
∴乙考上的概率为 ![]() ,丙考上的概率为
,丙考上的概率为 ![]() .
.
(2)解:由题意X的可能取值为1,2,
P(X=1)= ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() =
= ![]() ,
,
P(X=2)= ![]() =
= ![]() ,
,
∴X的分布列为:
X | 1 | 2 |
P |
|
|
EX= ![]() =
= ![]() .
.
【解析】(1)设A表示“甲考上”,B表示“乙考上”,C表示“丙考上”,由已知条件利用对立事件概率计算公式和相互独立事件概率乘法公式能求出乙、丙两人各自考上的概率.(2)由题意X的可能取值为1,3,分别求出相应的概率,由此能求出X的分布列和期望.
【考点精析】根据题目的已知条件,利用离散型随机变量及其分布列的相关知识可以得到问题的答案,需要掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.

练习册系列答案
相关题目