题目内容
(12分) 已知椭圆C: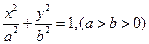 ,其相应于焦点
,其相应于焦点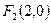 的准线方程为
的准线方程为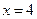 。
。 (Ⅰ)求椭圆C的方程;
(Ⅰ)求椭圆C的方程; (Ⅱ)已知过点
(Ⅱ)已知过点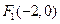 倾斜角为
倾斜角为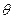 的直线分别交椭圆C于A、B两点,求证:
的直线分别交椭圆C于A、B两点,求证: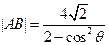 ;
; (Ⅲ)过点
(Ⅲ)过点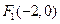 作两条互相垂直的直线分别交椭圆C于A、B和D、E,求
作两条互相垂直的直线分别交椭圆C于A、B和D、E,求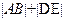 的最小值。
的最小值。
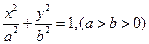 ,其相应于焦点
,其相应于焦点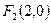 的准线方程为
的准线方程为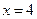 。
。 (Ⅰ)求椭圆C的方程;
(Ⅰ)求椭圆C的方程; (Ⅱ)已知过点
(Ⅱ)已知过点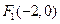 倾斜角为
倾斜角为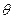 的直线分别交椭圆C于A、B两点,求证:
的直线分别交椭圆C于A、B两点,求证: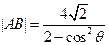 ;
; (Ⅲ)过点
(Ⅲ)过点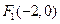 作两条互相垂直的直线分别交椭圆C于A、B和D、E,求
作两条互相垂直的直线分别交椭圆C于A、B和D、E,求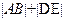 的最小值。
的最小值。(Ⅰ)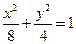 (Ⅱ)见解析 (Ⅲ)
(Ⅱ)见解析 (Ⅲ)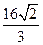
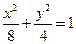 (Ⅱ)见解析 (Ⅲ)
(Ⅱ)见解析 (Ⅲ)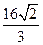
(Ⅰ)由题意得: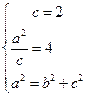 ,∴
,∴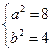 ,∴椭圆C的方程为
,∴椭圆C的方程为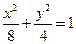 。
。
(Ⅱ)方法一:由(Ⅰ)知,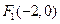 是椭圆C的左焦点,离心率
是椭圆C的左焦点,离心率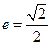 ,设
,设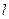 是椭圆的左准线,则
是椭圆的左准线,则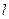 :
: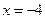 作
作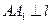 于
于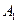 ,
,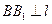 于
于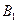 ,
,
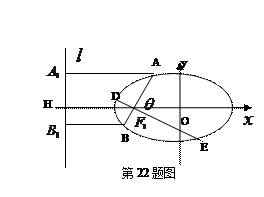
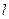 于
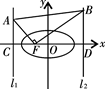
于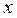 轴交于点H(如图),
轴交于点H(如图),
∵点A在椭圆上,∴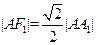
=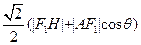 =
=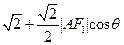
∴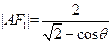 ,同理
,同理
∴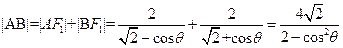 。
。
方法二:当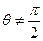 时,记
时,记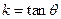 。则AB:
。则AB: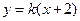
将其代入方程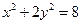 得
得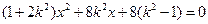
设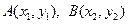 ,则
,则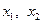 是此二次方程的两个根。∴
是此二次方程的两个根。∴ ,
,
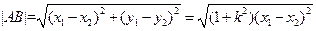
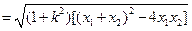
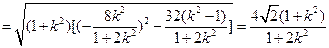 ①∵
①∵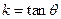 ,代入①式得
,代入①式得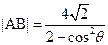 。②
。②
当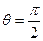 时,
时,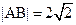 仍满足②式。∴
仍满足②式。∴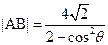 。
。
(Ⅲ)设直线AB倾斜角为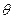 ,由于DE⊥AB,由(Ⅱ)可得
,由于DE⊥AB,由(Ⅱ)可得
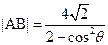 ,
,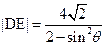 ,
,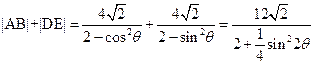
当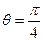 或
或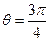 时,
时,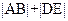 取得最小值
取得最小值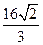 。
。
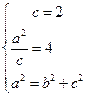 ,∴
,∴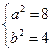 ,∴椭圆C的方程为
,∴椭圆C的方程为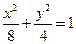 。
。(Ⅱ)方法一:由(Ⅰ)知,
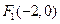 是椭圆C的左焦点,离心率
是椭圆C的左焦点,离心率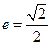 ,设
,设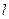 是椭圆的左准线,则
是椭圆的左准线,则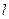 :
: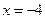 作
作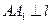 于
于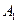 ,
,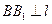 于
于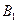 ,
,
 于
于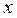 轴交于点H(如图),
轴交于点H(如图),∵点A在椭圆上,∴
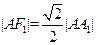
=
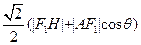 =
=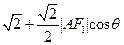
∴
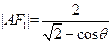 ,同理
,同理
∴
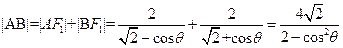 。
。方法二:当
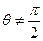 时,记
时,记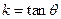 。则AB:
。则AB: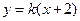
将其代入方程
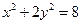 得
得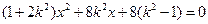
设
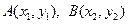 ,则
,则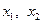 是此二次方程的两个根。∴
是此二次方程的两个根。∴ ,
,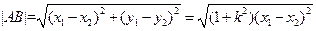
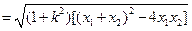
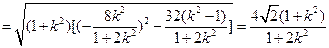 ①∵
①∵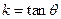 ,代入①式得
,代入①式得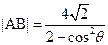 。②
。② 当
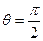 时,
时,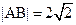 仍满足②式。∴
仍满足②式。∴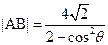 。
。(Ⅲ)设直线AB倾斜角为
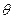 ,由于DE⊥AB,由(Ⅱ)可得
,由于DE⊥AB,由(Ⅱ)可得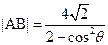 ,
,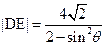 ,
,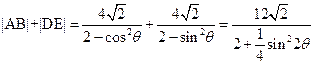
当
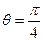 或
或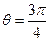 时,
时,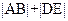 取得最小值
取得最小值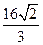 。
。
练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
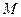 过点
过点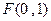 ,且与定圆
,且与定圆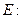
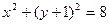 内切,动圆圆心
内切,动圆圆心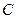 ,点
,点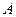 的坐标为
的坐标为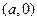 .
.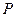 为曲线
为曲线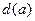 ;
;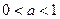 时,在(2)的条件下,设
时,在(2)的条件下,设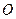 是坐标原点,
是坐标原点,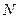 是曲线
是曲线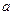 的点,记△
的点,记△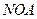 的面积为
的面积为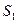 ,以
,以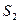 .若正数
.若正数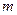 满足
满足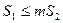 ,问
,问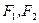 是椭圆
是椭圆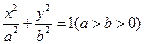 的两个焦点,
的两个焦点,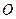 为坐标原点,点
为坐标原点,点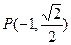 在椭圆上,且
在椭圆上,且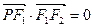 ,⊙
,⊙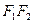 为直径的圆,直线
为直径的圆,直线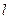 :
: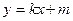 与⊙
与⊙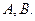
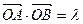 ,且满足
,且满足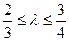 时,求弦长
时,求弦长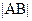 的取值范围.
的取值范围.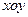 中,已知椭圆
中,已知椭圆 :
: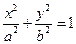
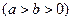 的离心率
的离心率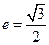 ,左、右两个焦点分别为
,左、右两个焦点分别为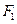 、
、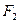 。过右焦点
。过右焦点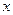 轴垂直的直线与椭圆
轴垂直的直线与椭圆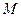 、
、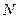 两点,且
两点,且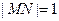 .
.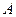 ,下顶点为
,下顶点为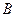 ,动点
,动点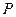 满足
满足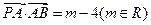 ,试求点
,试求点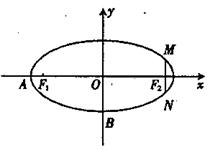
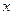 轴上的椭圆经过点M(1,
轴上的椭圆经过点M(1,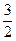 ),斜率为
),斜率为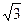 的直线经过椭圆的下顶点D和右焦点F,A、B为椭圆上不同于M的两点。
的直线经过椭圆的下顶点D和右焦点F,A、B为椭圆上不同于M的两点。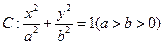 经过点
经过点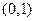 ,离心率
,离心率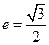 。
。
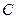 的方程;
的方程;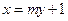 与椭圆
与椭圆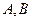 两点,点
两点,点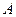 关于
关于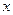 轴的对称点为
轴的对称点为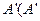 与
与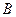 不重合),则直线
不重合),则直线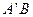 与
与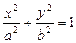 (
(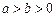 )的离心率为
)的离心率为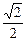 ,且短轴长为2.
,且短轴长为2.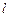 与椭圆交于
与椭圆交于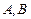 两点,
两点,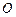 为坐标原点,且
为坐标原点,且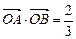 ,
,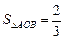 ,求直线
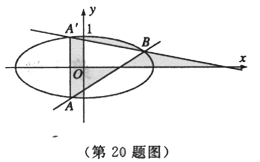
,求直线 的左、右准线分别为l1、l2,且分别交x轴于C、D两点,从l1上一点A发出一条光线经过椭圆的左焦点F被x轴反射后与l2交于点B,若
的左、右准线分别为l1、l2,且分别交x轴于C、D两点,从l1上一点A发出一条光线经过椭圆的左焦点F被x轴反射后与l2交于点B,若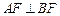 ,且
,且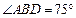 ,则椭圆的离心率等于_____________.
,则椭圆的离心率等于_____________.