题目内容
17.根据下列条件,求双曲线的标准方程.(1)与双曲线$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}$=1有共同的渐近线,一条准线为x=$\frac{18}{5}$;
(2)与双曲线$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{91}$=1有公共焦点,实轴长为18.
分析 (1)与双曲线$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}$=1有共同的渐近线,设方程为$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}$=λ,即$\frac{{x}^{2}}{9λ}-\frac{{y}^{2}}{16λ}=1$(λ>0),利用一条准线为x=$\frac{18}{5}$,求出λ,可得双曲线的标准方程;
(2)与双曲线$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{91}$=1有公共焦点,实轴长为18,可得c=10,a=9,即可求出双曲线的标准方程.
解答 解:(1)与双曲线$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}$=1有共同的渐近线,设方程为$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}$=λ,即$\frac{{x}^{2}}{9λ}-\frac{{y}^{2}}{16λ}=1$(λ>0),
∵一条准线为x=$\frac{18}{5}$,
∴$\frac{9λ}{5\sqrt{λ}}$=$\frac{18}{5}$,
∴λ=4,
∴方程为$\frac{{x}^{2}}{36}-\frac{{y}^{2}}{64}=1$;
(2)双曲线$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{91}$=1的焦点坐标为(±10,0),
∵与双曲线$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{91}$=1有公共焦点,实轴长为18,
∴c=10,a=9,
∴b=$\sqrt{19}$,
∴双曲线方程为$\frac{{x}^{2}}{81}-\frac{{y}^{2}}{19}=1$.
点评 本题考查双曲线的标准方程,考查双曲线的性质,考查学生分析解决问题的能力,属于中档题.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案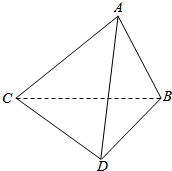 如图,在△ABC中,AB=AC,∠BAC=90°,△BCD中,∠CBD=90°,∠BDC=60°,BC=6,△ABC和△BCD相互垂直.
如图,在△ABC中,AB=AC,∠BAC=90°,△BCD中,∠CBD=90°,∠BDC=60°,BC=6,△ABC和△BCD相互垂直.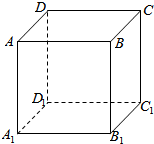 如图所示,在正方形ABCD-A1B1C1D1中:
如图所示,在正方形ABCD-A1B1C1D1中: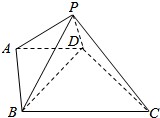 直角梯形ABCD中,∠ABC=90°,AB=AD=AP=1,BC=2,平面ABP垂直于底面ABCD.
直角梯形ABCD中,∠ABC=90°,AB=AD=AP=1,BC=2,平面ABP垂直于底面ABCD.