题目内容
设曲线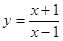 在点(3,2)处的切线与直线
在点(3,2)处的切线与直线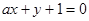 垂直,则a=( )
垂直,则a=( )
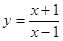 在点(3,2)处的切线与直线
在点(3,2)处的切线与直线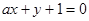 垂直,则a=( )
垂直,则a=( )| A.2 | B.-2 | C.-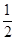 | D.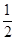 |
B
本试题主要是考查了导数的几何意义的运用。
因为函数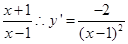 ,故可知函数在点(3,2)处的切线的斜率为-
,故可知函数在点(3,2)处的切线的斜率为-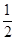 ,根据直线垂直时,斜率之积为-1,因此可知-a=2,a=-2,故选B.
,根据直线垂直时,斜率之积为-1,因此可知-a=2,a=-2,故选B.
解决该试题的关键是准确求解导数,并利用直线与直线的垂直关系得到斜率互为负倒数的关系求解参数a的值。
因为函数
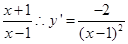 ,故可知函数在点(3,2)处的切线的斜率为-
,故可知函数在点(3,2)处的切线的斜率为-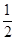 ,根据直线垂直时,斜率之积为-1,因此可知-a=2,a=-2,故选B.
,根据直线垂直时,斜率之积为-1,因此可知-a=2,a=-2,故选B.解决该试题的关键是准确求解导数,并利用直线与直线的垂直关系得到斜率互为负倒数的关系求解参数a的值。

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
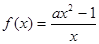 的单调增区间为(0,+∞),则实数
的单调增区间为(0,+∞),则实数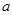 的取值范围是________.
的取值范围是________.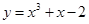 在点
在点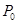 处的切线平行于直线
处的切线平行于直线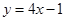 ,则点
,则点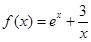 ,则此函数图像在点
,则此函数图像在点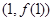 处的切线的倾斜角为( ).
处的切线的倾斜角为( ).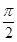
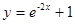 在点(0,2)处的切线与直线
在点(0,2)处的切线与直线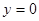 和
和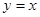 围成的三角形的面积
围成的三角形的面积 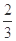
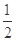
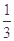
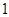
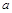 为实数,函数
为实数,函数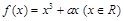 在
在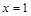 处有极值,则曲线
处有极值,则曲线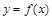 在原点处的切线方程为( )
在原点处的切线方程为( )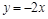
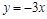
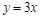
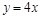
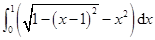 的值是( )
的值是( )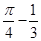 B.
B.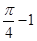 C.
C. D.
D.

 ,则函数( )
,则函数( ) 上是减函数
上是减函数