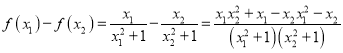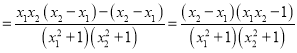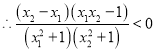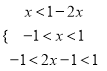题目内容

【题目】设a1 ， a2 ， …，an∈R，n≥3．若p：a1 ， a2 ， …，an成等比数列；q：（a +a +…+a ）（a +a +…+a ）=（a1a2+a2a3+…+an1an）2 ， 则p是q的条件．

【答案】充分不必要
【解析】解：由a1，a2，…，an∈R，n≥3．由柯西不等式，可得：

（a12+a22+…+an12）（a22+a32+…+an2）≥（a1a2+a2a3+…+an1an）2，

若a1，a2，…，an成等比数列，即有 = =…= ，

则（a12+a22+…+an12）（a22+a32+…+an2）=（a1a2+a2a3+…+an1an）2，

即由p推得q，

但由q推不到p，比如a1=a2=a3=…=an=0，则a1，a2，…，an不成等比数列．

故p是q的充分不必要条件．

所以答案是：充分不必要．

练习册系列答案
相关题目

【题目】电视连续剧《人民的名义》自2017年3月28日在湖南卫视开播以来，引发各方关注，收视率、点击率均占据各大排行榜首位．我们用简单随机抽样的方法对这部电视剧的观看情况进行抽样调查，共调查了600人，得到结果如下：其中图1是非常喜欢《人民的名义》这部电视剧的观众年龄的频率分布直方图；表1是不同年龄段的观众选择不同观看方式的人数．
表1

观看方式
年龄（岁）

电视

网络

150

250

120

80


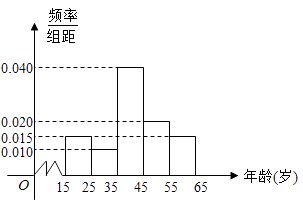
求：（I）假设同一组中的每个数据用该组区间的中点值代替，求非常喜欢《人民的名义》这部电视剧的观众的平均年龄；
（II）根据表1，通过计算说明我们是否有99%的把握认为观看该剧的方式与年龄有关？

0.50

0.40

0.25

0.15

0.10

0.05

0.025

0.010

0.005

0.001

0.455

0.708

1.323

2.072

2.706

3.841

5.024

6.635

7.879

10.828

附：

【题目】将函数y=cos2x的图象向左平移 个单位，得到函数y=f（x）cosx的图象，则f（x）的表达式可以是（ ）
A.f（x）=﹣2sinx
B.f（x）=2sinx
C.f（x）= sin2x
D.f（x）= （sin2x+cos2x）

【题目】已知函数.

（1）判断并证明函数的奇偶性；

（2）判断当时函数的单调性，并用定义证明；

（3）若定义域为，解不等式.

【答案】（1）奇函数（2）增函数（3）

【解析】试题分析：（1）判断与证明函数的奇偶性，首先要确定函数的定义域是否关于原点对称，再判断f(-x)与f(x)的关系，如果对定义域上的任意x，都满足f(-x)=f(x)就是偶函数，如果f(-x)=-f(x)就是奇函数，否则是非奇非偶函数。（2）利函数单调性定义证明单调性，按假设，作差，化简，判断，下结论五个步骤。（3）由（1）（2）奇函数在（-1，1）为单调函数，

原不等式变形为f(2x-1)<-f(x),即f(2x-1)<f(-x),再由函数的单调性及定义（-1，1）求解得x范围。

试题解析：（1）函数为奇函数．证明如下：

定义域为

又

为奇函数

（2）函数在（-1，1）为单调函数．证明如下：

任取，则

，

即

故在（-1，1）上为增函数

（3）由（1）、（2）可得

则

解得：

所以，原不等式的解集为

【点睛】

（1）奇偶性：判断与证明函数的奇偶性，首先要确定函数的定义域是否关于原点对称，再判断f(-x)与f(x)的关系，如果对定义域上的任意x，都满足f(-x)=f(x)就是偶函数，如果f(-x)=-f(x)就是奇函数，否则是非奇非偶函数。

（2）单调性：利函数单调性定义证明单调性，按假设，作差，化简，定号，下结论五个步骤。

【题型】解答题
【结束】
22

【题目】已知函数.

（1）若的定义域和值域均是，求实数的值；

（2）若在区间上是减函数，且对任意的，都有，求实数的取值范围；

（3）若，且对任意的，都存在，使得成立，求实数的取值范围.

【题目】已知：函数

求函数的周期T与单调增区间．

函数与的图象有几个公共交点．

设关于x的函数的最小值为，试确定满足的a的值．

【题目】已知定义在实数集R上的奇函数f（x）有最小正周期2，且当x∈（0，1）时， ．
（Ⅰ）求函数f（x）在（-1，1）上的解析式；
（Ⅱ）判断f（x）在（0，1）上的单调性；
（Ⅲ）当λ取何值时，方程f（x）=λ在（-1，1）上有实数解？

【题目】王先生家住 A 小区，他工作在 B 科技园区，从家开车到公司上班路上有 L1 ， L2 两条路线（如图），L1 路线上有 A1 ， A2 ， A3 三个路口，各路口遇到红灯的概率均为 ；L2 路线上有 B1 ， B2 两个路．各路口遇到红灯的概率依次为 ， ．若走 L1 路线，王先生最多遇到 1 次红灯的概率为；若走 L2 路线，王先生遇到红灯次数 X 的数学期望为 ．

【题目】在中，分别是角A、B、C的对边， ，且．

（1）求角A的大小； （2）求的值域．

【题目】设y=f(t)是某港口水的深度y(米)关于时间t(小时)的函数，其中.下表是该港口某一天从0时至24时记录的时间t与水深y的关系：

t

0

3

6

9

12

15

18

21

24

y

12

15.1

12.1

9.1

12

14.9

11.9

9

12.1

经长期观察，函数y=f(t)的图象可以近似地看成函数的图象.⑴求的解析式；⑵设水深不小于米时，轮船才能进出港口。某轮船在一昼夜内要进港口靠岸办事，然后再出港。问该轮船最多能在港口停靠多长时间？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网