题目内容
【题目】已知定义在实数集R上的奇函数f（x）有最小正周期2，且当x∈（0，1）时， 
．
（Ⅰ）求函数f（x）在（-1，1）上的解析式；
（Ⅱ）判断f（x）在（0，1）上的单调性；
（Ⅲ）当λ取何值时，方程f（x）=λ在（-1，1）上有实数解？
【答案】解：（Ⅰ）∵f（x）是x∈R上的奇函数，∴f（0）=0．
设x∈（-1，0），则-x∈（0，1），
= 
=f（x）
∴ 
∴ 
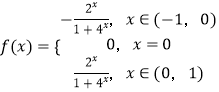
（Ⅱ）证明：设0＜x1＜x2＜1，
则 
，
∵0＜x1＜x2＜1，
∴ 
， 
，
∴f（x1）-f（x2）＞0
∴f（x）在（0，1）上为减函数．
（Ⅲ）解：∵f（x）在（0，1）上为减函数，
∴f（1）＜f（x）＜f（0）即 
同理，f（x）在（-1，0）上时，f（x） 
又f（0）=0
当 
或 
或λ=0时方程f（x）=λ在（-1，1）上有实数解．
【解析】（1）由于f（x）是定义域R上的奇函数，故一定有f（0）=0，设x∈（-1，0），则-x∈（0，1），根据f（-x）=-f（x），得出f（x）的解析式；（2）设0＜x1＜x2＜1，由单调函数的定义，着差证出f（x1）-f（x2）＞0，故f（x）在（0，1）上为减函数；（3）由二问可知f（x）在（0，1）上为减函数，得出f（x）在（0,1）的值域，同理得出（-1,0）的值域，又因为f（0）=0，不难得出当 λ ∈ ( 
， 
) 或 ( 
， 
) 或λ=0时方程f（x）=λ在（-1，1）上有实数解
【考点精析】利用函数奇偶性的性质和奇偶性与单调性的综合对题目进行判断即可得到答案，需要熟知在公共定义域内，偶函数的加减乘除仍为偶函数；奇函数的加减仍为奇函数；奇数个奇函数的乘除认为奇函数；偶数个奇函数的乘除为偶函数；一奇一偶的乘积是奇函数;复合函数的奇偶性：一个为偶就为偶，两个为奇才为奇；奇函数在关于原点对称的区间上有相同的单调性；偶函数在关于原点对称的区间上有相反的单调性．
