题目内容
2.已知函数f(x)是R上的奇函数,且f(-1)=0,若不等式$\frac{{x}_{1}f({x}_{1})-{x}_{2}f({x}_{2})}{{x}_{1}-{x}_{2}}$<0对区间(-∞,0)内任意两个不相等的实数x1、x2恒成立,则不等式2xf(3x)<0的解集是(-$\frac{1}{3}$,0)∪(0,$\frac{1}{3}$).分析 由$\frac{{x}_{1}f({x}_{1})-{x}_{2}f({x}_{2})}{{x}_{1}-{x}_{2}}$<0对区间(-∞,0)内任意两个不相等的实数x1,x2都成立,知g(x)=xf(x)在(-∞,0)上单调递减,由f(x)的奇偶性可判断g(x)的奇偶性及特殊点,从而可作出草图,由图象可解g(3x)<0,进而得到答案.
解答  解:∵$\frac{{x}_{1}f({x}_{1})-{x}_{2}f({x}_{2})}{{x}_{1}-{x}_{2}}$<0对区间(-∞,0)内任意两个不相等的实数x1,x2都成立,
解:∵$\frac{{x}_{1}f({x}_{1})-{x}_{2}f({x}_{2})}{{x}_{1}-{x}_{2}}$<0对区间(-∞,0)内任意两个不相等的实数x1,x2都成立,
∴函数g(x)=xf(x)在(-∞,0)上单调递减,
又 f(x)为奇函数,∴g(x)=xf(x)为偶函数,
g(x)在(0,+∞)上单调递增,且g(-1)=g(1)=0,
作出g(x)的草图如图所示:
2xf(3x)<0即g(3x)<0,
由图象得,-1<3x<0或0<3x<1,解得-$\frac{1}{3}$<x<0或0<x<$\frac{1}{3}$,
∴不等式2xf(3x)<0解集是(-$\frac{1}{3}$,0)∪(0,$\frac{1}{3}$),
故答案为:(-$\frac{1}{3}$,0)∪(0,$\frac{1}{3}$).
点评 本题考查函数的奇偶性、单调性及其应用,考查不等式的求解,综合运用函数性质化抽象不等式为具体不等式是解题关键.

练习册系列答案
相关题目
4.在△ABC中,已知sin2A=sin2B+sin2C,且sinA=2sinBcosC,则△ABC的形状是( )
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
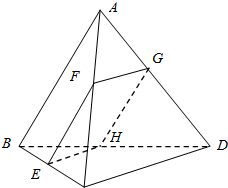 如图所示,在四面体ABCD中,截面EFGH平行于对于棱AB和CD,试问截面在什么位置时其截面面积最大?
如图所示,在四面体ABCD中,截面EFGH平行于对于棱AB和CD,试问截面在什么位置时其截面面积最大?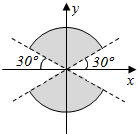 已知角β的终边在图中阴影所表示的范围内(不包括边界),那么β∈(K•180°+30°,K•180°+150°),k∈Z..
已知角β的终边在图中阴影所表示的范围内(不包括边界),那么β∈(K•180°+30°,K•180°+150°),k∈Z..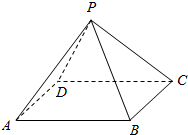 如图,P-ABCD是一个各棱长都为2cm的正四棱锥,求这个棱锥的表面积和体积.
如图,P-ABCD是一个各棱长都为2cm的正四棱锥,求这个棱锥的表面积和体积.