题目内容
如图,侧棱垂直底面的三棱柱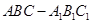 中,
中,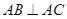 ,
,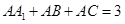 ,
,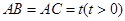 ,
,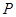 是侧棱
是侧棱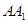 上的动点.
上的动点.
(1)当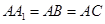 时,求证:
时,求证: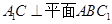 ;
;
(2)若二面角 的平面角的余弦值为
的平面角的余弦值为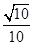 ,试求实数
,试求实数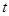 的值.
的值.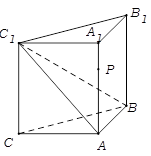
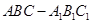 中,
中,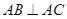 ,
,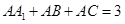 ,
,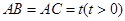 ,
,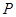 是侧棱
是侧棱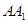 上的动点.
上的动点.(1)当
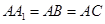 时,求证:
时,求证: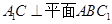 ;
;(2)若二面角
 的平面角的余弦值为
的平面角的余弦值为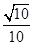 ,试求实数
,试求实数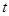 的值.
的值.
见解析.
第一问利用∵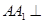 面
面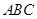 ,∴
,∴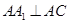 ,
,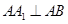 和∴四边形
和∴四边形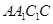 是正方形,∴
是正方形,∴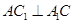 ∴
∴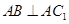 .
.
∵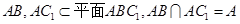 ,∴
,∴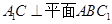
第二问中,分别以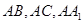 所在直线为
所在直线为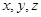 轴建立空间直角坐标系.则
轴建立空间直角坐标系.则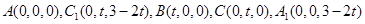 ,然后求解法向量表示二面角即可。
,然后求解法向量表示二面角即可。
解:(1)∵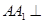 面
面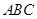 ,∴
,∴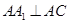 ,
,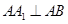 .
.
又∵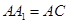 ,∴四边形
,∴四边形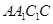 是正方形,∴
是正方形,∴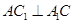 .
.
∵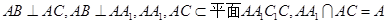 ,
,
∴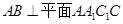 . 又∵
. 又∵ , ∴
, ∴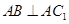 .
.
∵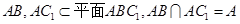 ,∴
,∴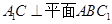 .
.
(2)分别以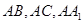 所在直线为
所在直线为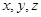 轴建立空间直角坐标系.则
轴建立空间直角坐标系.则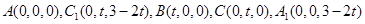
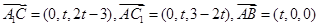 ,
,
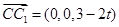 ,
,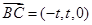 .
.
设平面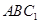 的法向量
的法向量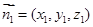 ,
,
则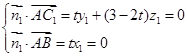 ,解得
,解得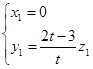 , 令
, 令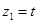 ,则
,则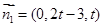 .
.
设平面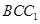 的法向量
的法向量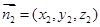 ,
,
则 .由于
.由于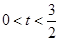 ,所以解得
,所以解得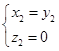 .
.
令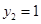 ,则
,则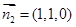 . 设二面角
. 设二面角 的平面角为
的平面角为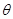 ,
,
则有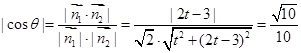 .
.
化简得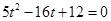 ,解得
,解得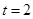 (舍去)或
(舍去)或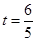 .
.
所以当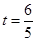 时,二面角
时,二面角 的平面角的余弦值为
的平面角的余弦值为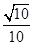 .
.
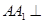 面
面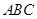 ,∴
,∴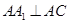 ,
,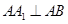 和∴四边形
和∴四边形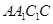 是正方形,∴
是正方形,∴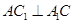 ∴
∴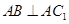 .
. ∵
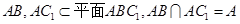 ,∴
,∴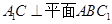
第二问中,分别以
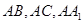 所在直线为
所在直线为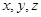 轴建立空间直角坐标系.则
轴建立空间直角坐标系.则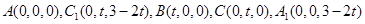 ,然后求解法向量表示二面角即可。
,然后求解法向量表示二面角即可。解:(1)∵
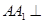 面
面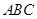 ,∴
,∴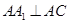 ,
,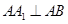 .
.又∵
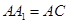 ,∴四边形
,∴四边形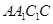 是正方形,∴
是正方形,∴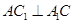 .
. ∵
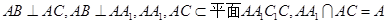 ,
,∴
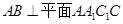 . 又∵
. 又∵ , ∴
, ∴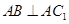 .
. ∵
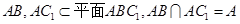 ,∴
,∴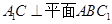 .
. (2)分别以
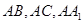 所在直线为
所在直线为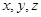 轴建立空间直角坐标系.则
轴建立空间直角坐标系.则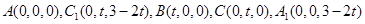
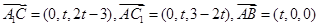 ,
,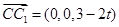 ,
,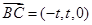 .
. 设平面
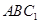 的法向量
的法向量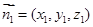 ,
,则
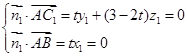 ,解得
,解得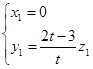 , 令
, 令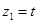 ,则
,则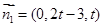 .
. 设平面
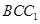 的法向量
的法向量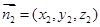 ,
,则
 .由于
.由于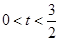 ,所以解得
,所以解得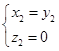 .
.令
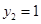 ,则
,则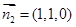 . 设二面角
. 设二面角 的平面角为
的平面角为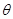 ,
,则有
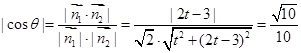 .
.化简得
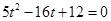 ,解得
,解得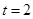 (舍去)或
(舍去)或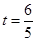 .
.所以当
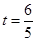 时,二面角
时,二面角 的平面角的余弦值为
的平面角的余弦值为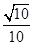 .
.
练习册系列答案
相关题目
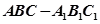 中,
中,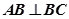 ,
,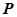 为
为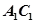 的中点,且
的中点,且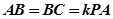 ,
,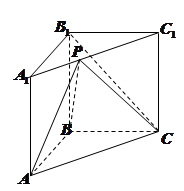
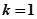 时,求证:
时,求证: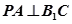 ;
;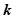 为何值时,直线
为何值时,直线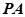 与平面
与平面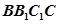 所成的角的正弦值为
所成的角的正弦值为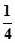 ,并求此时二面角
,并求此时二面角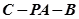 的余弦值。
的余弦值。 的大小的余弦值.
的大小的余弦值.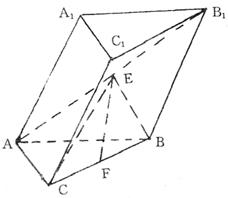
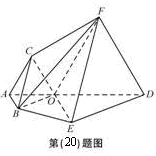
 为多面体,平面
为多面体,平面 与平面
与平面 垂直,点
垂直,点 在线段
在线段 上,
上,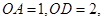 △OAB,,△
△OAB,,△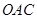 ,△
,△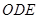 ,△
,△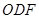 都是正三角形。
都是正三角形。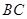 ∥
∥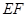 ;
;
 中,
中, 是
是 的中点,
的中点, 是线段
是线段 上一点,且
上一点,且 .
. ;
; 平面
平面 ,求
,求 的值.[
的值.[
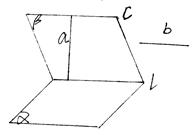
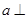 直线
直线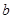 ,a,b异面,
,a,b异面,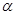 ,
,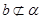 。求证:
。求证: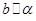 。
。
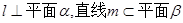 ,有下面四个命题:
,有下面四个命题: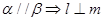 ;(2)
;(2)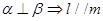 ;(3)
;(3)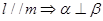 ;(4)
;(4)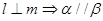
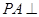 ⊙O,C为圆周上一点,若
⊙O,C为圆周上一点,若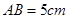 ,
,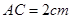 ,则B点到平面PAC的距离为 。
,则B点到平面PAC的距离为 。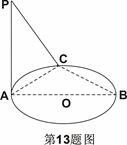
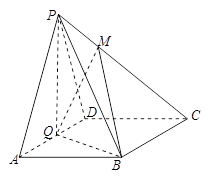
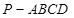 中,底面
中,底面 为菱形,
为菱形,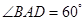 ,
,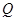 为
为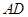 的中点,
的中点,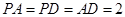 .
.
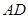
 平面
平面 ;
;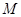 在线段
在线段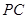 上,
上,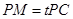 ,试确定
,试确定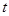 的值,使
的值,使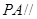 平面
平面 ;
;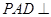 平面
平面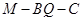 的大小.
的大小.