题目内容
【题目】已知函数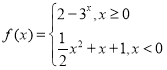
（1）写出函数
的单调区间；
（2）若函数
恰有3个不同零点，求实数
的取值范围；
（3）若
对所有
恒成立，求实数
的取值范围.
【答案】（1）单调减区间为
，
，增区间为
，（2）
，（3）
【解析】
（1）画出函数
的图像即可求出函数的单调区间.
（2）转化为函数
的图像与
恰有
个不同的交点，利用函数的图像即可求出
的取值范围.
（3）将题意转化为
，再求出
，转化为
在
恒成立，从而建立关于
的不等关系，解不等式组即可.
（1）函数的图像如图所示：
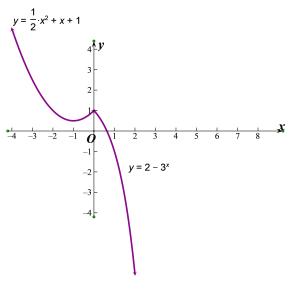
由图知：函数的单调减区间为，，增区间为.
（2）函数
恰有3个不同零点，
等价于：函数的图像与恰有个不同的交点.
因为
，
由图知：
，即.
（3）
对所有
恒成立，
等价于即可.
由函数的图像知，，
所以等价于：在恒成立.
所以
或
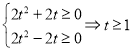或
.
所以的取值范围是.
【题目】现对某市工薪阶层关于“楼市限购令”的态度进行调查，随机抽调了50人，他们月收入的频数分布及对“楼市限购令”赞成人数如下表.
月收入(单位百元) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
(1)由以上统计数据填下面2×2列联表，并问是否有99％的把握认为“月收入以5500元为分界点对“楼市限购令”的态度有差异；
月收入不低于55百元的人数 | 月收入低于55百元的人数 | 合计 | |
赞成 | a=______________ | c=______________ | ______________ |
不赞成 | b=______________ | d=______________ | ______________ |
合计 | ______________ | ______________ | ______________ |
(2)试求从年收入位于
（单位：百元）的区间段的被调查者中随机抽取2人，恰有1位是赞成者的概率。
参考公式：
，其中
.
参考值表：
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
