题目内容
【题目】甲、乙两位学生参加数学竞赛培训,在培训期间,他们参加的5项预赛成绩记录如下:

(1)用茎叶图表示这两组数据;
(2)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(3)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?说明理由.
【答案】(1) 茎叶图见解析;(2)![]() ;(3) 派甲.
;(3) 派甲.
【解析】
(1)两位数的茎叶图,十位为茎、个位为叶
(2)枚举法,写出所有的基本事件,利用P(A)=![]()
(3)选人参加比赛,首先比较平均数,平均数大的选中,若平均数一样,再比较方差,选方差小的更稳点
(1)作出茎叶图如下:
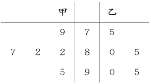
(2)记甲被抽到的成绩为x,乙被抽到的成绩为y,用数对(x,y)表示基本事件:
(82,95) (82,75) (82,80) (82,90) (82,85)
(82,95) (82,75) (82,80) (82,90) (82,85)
(79,95) (79,75) (79,80) (79,90) (79,85)
(95,95) (95,75) (95,80) (95,90) (95,85)
(87,95) (87,75) (87,80) (87,90) (87,85)
基本事件总数n=25.
记“甲的成绩比乙高”为事件A,事件A包含的基本事件:
(82,75) (82,80) (82,75) (82,80) (79,75)
(95,75) (95,80) (95,90) (95,85) (87,75) (87,80) (87,85)
事件A包含的基本事件数m=12.
所以P(A)=![]() =
=![]() .(以上两问可用计数原理完成).
.(以上两问可用计数原理完成).
(3)派甲参赛比较合适.理由如下:![]()
![]() ,
,
∴甲的成绩较稳定,派甲参赛比较合适.

【题目】我校为了解学生喜欢通用技术课程“机器人制作”是否与学生性别有关,采用简单随机抽样的办法在我校高一年级抽出一个有60人的班级进行问卷调查,得到如下的![]() 列联表:
列联表:
喜欢 | 不喜欢 | 合计 | |
男生 | 18 | ||
女生 | 6 | ||
合计 | 60 |
已知从该班随机抽取1人为喜欢的概率是![]() .
.
(Ⅰ)请完成上面的![]() 列联表;
列联表;
(Ⅱ)根据列联表的数据,若按90%的可靠性要求,能否认为“喜欢与否和学生性别有关”?请说明理由.
参考临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() 其中
其中![]()
【题目】某研究性学习小组为了调查研究学生玩手机对学习的影响,现抽取了30名学生,得到数据如表:
玩手机 | 不玩手机 | 合计 | |
学习成绩优秀 | 8 | ||
学习成绩不优秀 | 16 | ||
合计 | 30 |
已知在全部的30人中随机抽取1人,抽到不玩手机的概率为![]() .
.
(1)请将2×2列联表补充完整;
(2)能否在犯错误的概率不超过0.005的前提下认为玩手机对学习有影响;
(3)现从不玩手机,学习成绩优秀的8名学生中任意选取两人,对他们的学习情况进行全程跟踪,记甲、乙两名学生被抽到的人数为X,求X的分布列和数学期望.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() .
.