题目内容
①命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”;②若P且Q为假命题,则P、Q均为假命题;
③在△ABC中,sinA>sinB的充要条件是A>B;
④不等式的解集为|x|+|x-1|>a的解集为R,则a≤1;
⑤点(x,y)在映射f作用下的象是(2x,
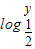 ),则在f的作用下,点(1,-1)的原象是(0,2).
),则在f的作用下,点(1,-1)的原象是(0,2).其中真命题的是 (写出所有真命题的编号)
【答案】分析:本题考查的知识点是四种命题间的逆否关系,充要条件的定义,映射的定义及绝对值不等式的解法,根据上述定义逐一分析5个命题,判断它们的真假即可得到结论.
解答:解:命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”,故①正确.
若P且Q为假命题,则P、Q至少有一个是假命题,故②错误;
在△ABC中,sinA>sinB?a>b?A>B,故③正确;
不等式的解集为|x|+|x-1|>a的解集为R,则a<1,故④错误;
点(x,y)在映射f作用下的象是(2x,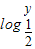 ),则在f的作用下,点(1,-1)的原象是(0,2),故⑤正确.
),则在f的作用下,点(1,-1)的原象是(0,2),故⑤正确.
故答案为:①③⑤
点评::已知原命题,写出它的其他三种命题,首先把原命题改写成“若p,则q”的形式,然后找出其条件p和结论q,再根据四种命题的定义写出其他命题.逆命题:“若q,则p”;否命题:“若¬p,则¬q”;逆否命题:“若¬q,则¬p”,对写出的命题也可简洁表述;对于含有大前提的命题,在改写命题形式时,大前提不要动.
解答:解:命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”,故①正确.
若P且Q为假命题,则P、Q至少有一个是假命题,故②错误;
在△ABC中,sinA>sinB?a>b?A>B,故③正确;
不等式的解集为|x|+|x-1|>a的解集为R,则a<1,故④错误;
点(x,y)在映射f作用下的象是(2x,
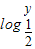 ),则在f的作用下,点(1,-1)的原象是(0,2),故⑤正确.
),则在f的作用下,点(1,-1)的原象是(0,2),故⑤正确.故答案为:①③⑤
点评::已知原命题,写出它的其他三种命题,首先把原命题改写成“若p,则q”的形式,然后找出其条件p和结论q,再根据四种命题的定义写出其他命题.逆命题:“若q,则p”;否命题:“若¬p,则¬q”;逆否命题:“若¬q,则¬p”,对写出的命题也可简洁表述;对于含有大前提的命题,在改写命题形式时,大前提不要动.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目