题目内容
18．已知长方体ABCD-A1B1C1D1的体积为216，则四面体AB1CD1与四面体A1BC1D的重叠部分的体积为36．分析 由题意画出图形，得到四面体AB1CD1与四面体A1BC1D的重叠部分的形状，由棱锥体积公式得答案．
解答 解：如图所示，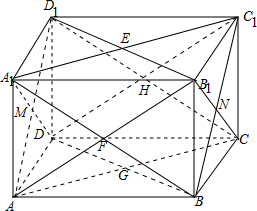
四面体AB1CD1与四面体A1BC1D的重叠部分是以长方体各面中心为定点的多面体，
摘出如图，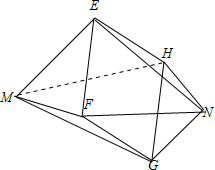
设长方体的过同一顶点的三条棱长分别为a，b，c，则abc=216，
重叠部分的体积为两个同底面的四棱锥体积和，等于$\frac{1}{3}×\frac{1}{2}abc=\frac{1}{6}×216=36$．
故答案为：36．
点评 本题考查了棱柱的结构特征，考查了学生的空间想象能力和思维能力，是中档题．
练习册系列答案
相关题目
6．在长方体ABCD-A1B1C1D1中，AB=BC=2，AA1=1，若E，F为BD1的两个三等分点，G为长方体ABCD-A1B1C1D1表面上的动点，则∠EGF的最大值是（ ）
| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
13．
一家面包房根据以往某种面包的销售记录，绘制了日销售量的频率分布直方图如图所示：老板根据销售量给以店员奖励，具体奖励规定如表：
（1）求在未来连续3天里，店员共获得奖励150元的概率
（2）记未来连续2天，店员获得奖励X元，求随机变量X的分布列及数学期望EX．
一家面包房根据以往某种面包的销售记录，绘制了日销售量的频率分布直方图如图所示：老板根据销售量给以店员奖励，具体奖励规定如表：| 销售量X个 | X＜100 | 100≤X＜150 | 150≤X＜200 | X≥200 |
| 奖励金额（元） | 0 | 50 | 100 | 150 |
（2）记未来连续2天，店员获得奖励X元，求随机变量X的分布列及数学期望EX．
在四面体ABCD中，若AB=AD，CD=BC，求证：AC⊥BD．
8．设函数f（x）=exsinx-cosx，g（x）=xcosx-$\sqrt{2}$ex（其中e是自然对数的底数），?x1∈[0，$\frac{π}{2}$]，?x2∈[0，$\frac{π}{2}$]，使得不等式f（x1）+g（x2）≥m成立，则实数m的范围（ ）
| A． | （-∞，-1-$\sqrt{2}$] | B． | （-∞，${e}^{\frac{π}{2}}$-$\sqrt{2}$] | C． | （-∞，-1-$\sqrt{2}$${e}^{\frac{π}{2}}$] | D． | （-∞，（-1-$\sqrt{2}$）${e}^{\frac{π}{2}}$] |