题目内容
17．在四面体ABCD中，棱长AB=$\sqrt{5}$，其余棱长都是$\sqrt{3}$，求这个四面体的体积以及其外接球的半径．分析 由题意画出图形，取CD中点G，把四面体体积转化为两个三棱锥D-ABG、C-ABG的体积求解；由题目所给四面体的对称性及其外接球的对称性可知取AB中点Q，连接GQ，由对称性可知，四面体ABCD外接球的球心O在GQ上，由于勾股定理，计算即可得到半径R．
解答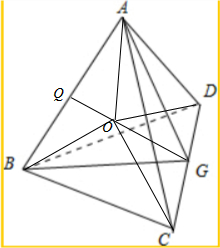 
解：如图，取CD中点G，∵△ACD、△BCD都是边长为$\sqrt{3}$的正三角形，
∴AG=BG=$\frac{3}{2}$，
在等腰三角形AGB中，又AB=$\sqrt{5}$，∴G到AB的距离为$\sqrt{（\frac{3}{2}）^{2}-（\frac{\sqrt{5}}{2}）^{2}}=1$，
则${S}_{△AGB}=\frac{1}{2}×\sqrt{5}×1=\frac{\sqrt{5}}{2}$，
∴${V}_{ABCD}=\frac{1}{3}×\frac{\sqrt{5}}{2}×\sqrt{3}=\frac{\sqrt{15}}{6}$；
取AB中点Q，连接GQ，
由对称性可知，四面体ABCD外接球的球心O在GQ上，
由勾股定理可得$\sqrt{{R}^{2}-（\frac{\sqrt{5}}{2}）^{2}}$+$\sqrt{{R}^{2}-（\frac{\sqrt{3}}{2}）^{2}}$=1，
解得R=$\frac{\sqrt{21}}{4}$．
点评 本小题主要考查空间线面关系、几何体的体积等知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力，训练了正弦定理和余弦定理的应用，是中档题．
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
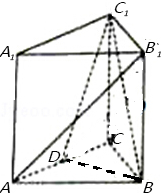如图，在直三棱柱ABC-A1B1C1中，底面为等边三角形，D为AC的中点，AA1=AB=6．
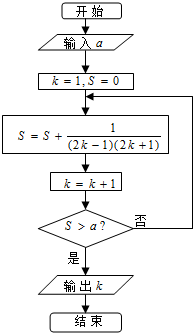阅读如图所示的程序框图，若输入a的值为二项（$\sqrt{x}$+$\frac{1}{19{x}^{4}}$）9展开式的常数项，则输出的k值为9．
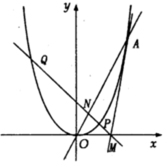在平面直角坐标系xOy中，已知抛物线x2=2py（p＞0）的准线方程为y=-$\frac{1}{2}$，过点M（4，0）作抛物线的切线MA，切点为A（异于点O），直线l过点M与抛物线交于两点P、Q，与直线OA交于点N．
12．已知函数f（x）=x3-3x，x∈R，若方程f（x）=k|x-$\sqrt{3}$|恰有3个互异的实数根，则实数k的取值范围是（ ）
| A． | （-$\frac{3}{4}$，6） | B． | （-6，$\frac{3}{4}$） | C． | （-∞，-6）∪（$\frac{3}{4}$，+∞） | D． | （-∞，-$\frac{3}{4}$）∪（6，+∞） |
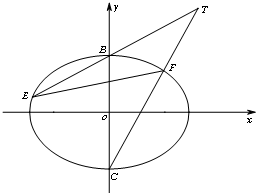如图，已知椭圆M：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0），焦距为2c（c＞0），其离心率为$\frac{{\sqrt{3}}}{2}$，$\frac{a^2}{c}=\frac{{4\sqrt{3}}}{3}$．B，C分别为椭圆M的上、下顶点，过点T（t，2）（t≠0）的直线TB，TC分别交椭圆M于E，F两点．