题目内容
8.已知集合A={x|x2-3x+2=0,x∈R},B={x|x2-ax+2=0,x∈R},若B⊆A,求实数a的取值范围.分析 先确定集合A的元素,利用B⊆A,确定a的取值.
解答 解:因为A={x|x2-3x+2=0}={1,2},所以要使B⊆A,则有
①若B=∅,则△=a2-8<0,解得-2$\sqrt{2}$<a<2$\sqrt{2}$.
②若B≠∅,则B={1}或B={2}或B={1,2}.
若B={1},$\left\{\begin{array}{l}{△=0}\\{1-a+2=0}\end{array}\right.$即$\left\{\begin{array}{l}{a=±2\sqrt{2}}\\{a=3}\end{array}\right.$无解舍去
若B={2},$\left\{\begin{array}{l}{△=0}\\{4-2a+2=0}\end{array}\right.$无解舍去
若B={1,2},$\left\{\begin{array}{l}{△>0}\\{a=3}\end{array}\right.$解得a=3
综上:a的取值范围是-2$\sqrt{2}$<a<2$\sqrt{2}$或a=3.
点评 本题主要考查利用集合之间的关系确定参数的取值范围,要注意分类讨论.属于基础题型.

练习册系列答案
相关题目
16.一个正方体的对角线长为3$\sqrt{3}$,则这个正方体的棱长为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
3.已知函数f(x)=2ln x-xf′(1),则曲线y=f(x)在x=1处的切线方程是( )
| A. | x-y+2=0 | B. | x+y+2=0 | C. | x+y-2=0 | D. | x-y-2=0 |
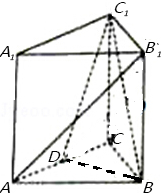 如图,在直三棱柱ABC-A1B1C1中,底面为等边三角形,D为AC的中点,AA1=AB=6.
如图,在直三棱柱ABC-A1B1C1中,底面为等边三角形,D为AC的中点,AA1=AB=6.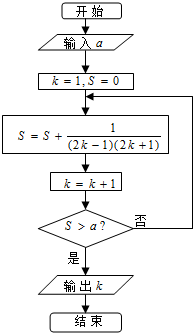 阅读如图所示的程序框图,若输入a的值为二项($\sqrt{x}$+$\frac{1}{19{x}^{4}}$)9展开式的常数项,则输出的k值为9.
阅读如图所示的程序框图,若输入a的值为二项($\sqrt{x}$+$\frac{1}{19{x}^{4}}$)9展开式的常数项,则输出的k值为9.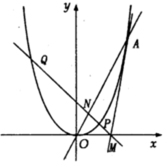 在平面直角坐标系xOy中,已知抛物线x2=2py(p>0)的准线方程为y=-$\frac{1}{2}$,过点M(4,0)作抛物线的切线MA,切点为A(异于点O),直线l过点M与抛物线交于两点P、Q,与直线OA交于点N.
在平面直角坐标系xOy中,已知抛物线x2=2py(p>0)的准线方程为y=-$\frac{1}{2}$,过点M(4,0)作抛物线的切线MA,切点为A(异于点O),直线l过点M与抛物线交于两点P、Q,与直线OA交于点N.