题目内容
16. 如图,四棱锥P-ABCD的底面ABCD是平行四边形,侧面PAD是等边三角形,平面PAD⊥平面ABCD,M,N分别是棱PC,AB的中点,且MN⊥CD.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,侧面PAD是等边三角形,平面PAD⊥平面ABCD,M,N分别是棱PC,AB的中点,且MN⊥CD.(Ⅰ)求证:AD⊥CD;
(Ⅱ)若AB=AD,求直线MN与平面PBD所成角的正弦值.
分析 (Ⅰ)取PD边中点E,连接AE,EM,根据MN⊥CD容易得到CD⊥AE,而根据已知条件可以说明PO⊥平面ABCD,从而得到CD⊥PO,这样CD就垂直于平面PAD内两条相交直线,由线面垂直的判定定理从而得到AD⊥CD;
(Ⅱ)取BC中点F,连接OF,由(Ⅰ)便可知道OA,OF,OP三条直线两两垂直,从而可分别以这三条直线为x,y,z轴,可设AB=2,这样即可求得图形中一些点的坐标.从而求出向量$\overrightarrow{DB},\overrightarrow{DP}$的坐标,这时候设平面PBD的法向量为$\overrightarrow{n}=(x,y,z)$,根据$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DB}=0}\\{\overrightarrow{n}•\overrightarrow{DP}=0}\end{array}\right.$即可求出$\overrightarrow{n}$的坐标,若设MN和平面PBD所成角为θ,从而根据sinθ=$|cos<\overrightarrow{n},\overrightarrow{MN}>|=|\frac{\overrightarrow{n}•\overrightarrow{MN}}{|\overrightarrow{n}||\overrightarrow{MN}|}|$即可求得答案.
解答 解:(Ⅰ)证明:如图,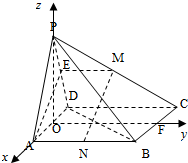
取PD中点E,连AE,EM,则EM∥AN,且EM=AN;
∴四边形ANME是平行四边形,MN∥AE;
∵MN⊥CD,∴AE⊥CD,即CD⊥AE;
取AD中点O,连PO,△PAD是等边三角形,则PO⊥AD;
又因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD;
∴PO⊥平面ABCD,PO⊥CD,即CD⊥PO;
故CD⊥平面PAD,AD?平面PAD;
∴CD⊥AD,即AD⊥CD;
(Ⅱ)由AB=AD,AD⊥CD,得?ABCD是正方形;
取BC边的中点F,连接OF,则分别以OA,OF,OP所在直线为x,y,z轴建立如图所示空间直角坐标系;
设AB=2,则A(1,0,0),B(1,2,0),D(-1,0,0),P(0,0,$\sqrt{3}$),E(-$\frac{1}{2}$,0,$\frac{\sqrt{3}}{2}$);
$\overrightarrow{DB}$=(2,2,0),$\overrightarrow{DP}$=(1,0,$\sqrt{3}$);
设平面PBD的法向量$\overrightarrow{n}=(x,y,z)$,则:
$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DB}=0}\\{\overrightarrow{n}•\overrightarrow{DP}=0}\end{array}\right.$;
∴$\left\{\begin{array}{l}{2x+2y=0}\\{x+\sqrt{3}z=0}\end{array}\right.$;
∴$\left\{\begin{array}{l}{x=-\sqrt{3}z}\\{y=\sqrt{3}z}\end{array}\right.$,取z=1,∴$\overrightarrow{n}=(-\sqrt{3},\sqrt{3},1)$;
$\overrightarrow{MN}$=$\overrightarrow{EA}$=($\frac{3}{2}$,0,-$\frac{\sqrt{3}}{2}$);
设直线MN与平面PBD所成的角为θ,则:
sinθ=|cos<$\overrightarrow{MN}$,$\overrightarrow{n}$>|=$\frac{2\sqrt{3}}{\sqrt{7}•\sqrt{3}}$=$\frac{2\sqrt{7}}{7}$.
点评 考查面面垂直的性质定理,线面垂直的判定定理,以及建立空间直角坐标系,利用向量解决直线和平面所成角的问题,能求空间点的坐标,注意线面角和直线和平面法向量所成角的关系,以及向量夹角余弦的坐标公式.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案| A. | (0,1) | B. | (-2,0)∪(0,1) | C. | (-2,-$\frac{1}{2}$)∪(-$\frac{1}{2}$,1) | D. | (-2,1) |
 已知AB是⊙O的直径,直线AF交⊙O于F(不与B重合),直线EC与⊙O相切于C,交AB于E,连接AC,且∠OAC=∠CAF,求证:
已知AB是⊙O的直径,直线AF交⊙O于F(不与B重合),直线EC与⊙O相切于C,交AB于E,连接AC,且∠OAC=∠CAF,求证: 把公差为2的等差数列{an}的各项依次插入等比数列{bn}的第1项、第2项、…、第n项后,得到数列{cn}:b1,a1,b2,a2,b3,a3,b4,a4,…,记数列{cn}的前n项和为Sn,已知c1=1,c2=3,S3=$\frac{17}{4}$.
把公差为2的等差数列{an}的各项依次插入等比数列{bn}的第1项、第2项、…、第n项后,得到数列{cn}:b1,a1,b2,a2,b3,a3,b4,a4,…,记数列{cn}的前n项和为Sn,已知c1=1,c2=3,S3=$\frac{17}{4}$.