题目内容
11.若函数f(x)的图象从左到右先增后减,则称函数f(x)为“∩型”函数,图象的最高点的横坐标称为“∩点”.(1)若函数f(x)=lnx-$\frac{1}{2m}$(x2-1)为“∩型”函数,试求实数m的取值范围,并求出此时的“∩点”.
(2)若g(x)=x-lnx,试证明:$\sum_{k=2}^{n}$$\frac{1}{k-g(k)}$>$\frac{3{n}^{2}-n-2}{n(n+1)}$(n∈N,n≥2)
分析 (1)通过“∩型”函数的定义,分m<0、m>0两种情况讨论即可;
(2)通过令m=2,即f(x)=$lnx-\frac{1}{4}({x}^{2}-1)$,及f(x)在[$\sqrt{2}$,+∞)上单减可得f(x)<0,化简得$\frac{1}{lnx}>2(\frac{1}{x-1}-\frac{1}{x+1})$,累加即可.
解答 解:(1)$f′(x)=\frac{1}{x}-\frac{x}{m}=-\frac{{x}^{2}-m}{mx}$,
①当m<0时,f′(x)>0对x∈(0,+∞)恒成立,
∴f(x)在(0,+∞)上为增函数,此时f(x)不是“∩型”函数;
②当m>0时,f(x)、f′(x)的变化情况如下表
| x | $(0,\sqrt{m})$ | $\sqrt{m}$ | $(\sqrt{m},+∞)$ |
| f′(x) | + | 0 | - |
| f(x) | ↑ | ↓ |
综上所述,当m>0时,函数f(x)为“∩型”函数,“∩点”为$\sqrt{m}$.
(2)∵g(x)=x-lnx,∴k-g(k)=lnk,
∴$\sum_{k=2}^{n}$$\frac{1}{k-g(k)}$>$\frac{3{n}^{2}-n-2}{n(n+1)}$(n∈N,n≥2)?$\frac{1}{ln2}$+$\frac{1}{ln3}$+…+$\frac{1}{lnn}$>$\frac{3{n}^{2}-n-2}{n(n+1)}$,
在f(x)中,令m=2,则f(x)=$lnx-\frac{1}{4}({x}^{2}-1)$,
由(1)知,f(x)在[$\sqrt{2}$,+∞)上为减函数,
∴当x≥2时,f(x)≤f(2)=$ln2-\frac{3}{4}$<0,故$lnx<\frac{1}{4}({x}^{2}-1)$,
因此当x≥2时,$\frac{1}{lnx}>\frac{4}{{x}^{2}-1}=2(\frac{1}{x-1}-\frac{1}{x+1})$,
∴$\frac{1}{ln2}$+$\frac{1}{ln3}$+…+$\frac{1}{lnn}$>$2[(1-\frac{1}{3})+(\frac{1}{2}-\frac{1}{4})$$+(\frac{1}{3}-\frac{1}{5})+…+(\frac{1}{n-1}-\frac{1}{n+1})]$
=$2(1+\frac{1}{2}-\frac{1}{n}-\frac{1}{n+1})$
=$\frac{3{n}^{2}-n-2}{n(n+1)}$,
即$\sum_{k=2}^{n}$$\frac{1}{k-g(k)}$>$\frac{3{n}^{2}-n-2}{n(n+1)}$(n∈N,n≥2).
点评 本题考查新定义函数,函数的单调性,累加法,对表达式进行灵活变形是解决本题的关键,注意解题方法的积累,属于难题.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
1.已知空间两条直线a、b没有公共点,则a和b( )
| A. | 一定是异面直线 | B. | 一定是平行直线 | ||
| C. | 不可能是平行直线 | D. | 不可能是相交直线 |
2.在△ABC中,若tan$\frac{A}{2}$,tan$\frac{B}{2}$,tan$\frac{C}{2}$成等比数列,则角B的取值范围是( )
| A. | (0,$\frac{π}{6}$] | B. | [$\frac{π}{3}$,$\frac{2π}{3}$] | C. | (0,$\frac{π}{3}$] | D. | [$\frac{2π}{3}$,π) |
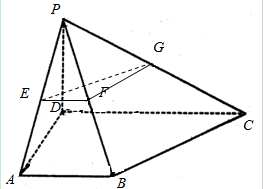 如图,在四棱锥P-ABCD的底面为直角梯形,且∠BAD=∠ADC=90°,E,F,G分别为PA,PB,PC的中点,直线PB⊥平面EFG,AB=$\frac{1}{3}$DC=$\frac{1}{3}$AD=1.
如图,在四棱锥P-ABCD的底面为直角梯形,且∠BAD=∠ADC=90°,E,F,G分别为PA,PB,PC的中点,直线PB⊥平面EFG,AB=$\frac{1}{3}$DC=$\frac{1}{3}$AD=1. 如图,四棱锥P-ABCD的底面ABCD是平行四边形,侧面PAD是等边三角形,平面PAD⊥平面ABCD,M,N分别是棱PC,AB的中点,且MN⊥CD.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,侧面PAD是等边三角形,平面PAD⊥平面ABCD,M,N分别是棱PC,AB的中点,且MN⊥CD. 在三棱柱ABC-A1B1C1中,底面ABC为正三角形,A1在底面ABC上的射影是棱BC的中点O,OE⊥AA1于E点.
在三棱柱ABC-A1B1C1中,底面ABC为正三角形,A1在底面ABC上的射影是棱BC的中点O,OE⊥AA1于E点.