题目内容
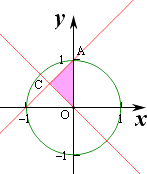
【题目】在平面直角坐标系xOy中，D是到原点的距离不大于1的点构成的区域，E是满足不等式组 
的点（x，y）构成的区域，向D中随机投一点，则所投的点落在E中的概率是 ．
【答案】
【解析】解：区域D对应的平面区域为半径为1的圆，面积为S=π，
区域E对应的区域为三角形AOC，
由 
，解得 
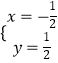，即C（ 
），
A（0，1），
则三角形AOC的面积S= 
，
则对应的概率为 
= ，
所以答案是： ．
【考点精析】通过灵活运用二元一次不等式（组）所表示的平面区域和几何概型，掌握不等式组表示的平面区域是各个不等式所表示的平面区域的公共部；几何概型的特点：1）试验中所有可能出现的结果（基本事件）有无限多个；2）每个基本事件出现的可能性相等即可以解答此题．
练习册系列答案
相关题目
【题目】在某次试验中，两个试验数据x，y的统计结果如下面的表格1所示．
x | 1 | 2 | 3 | 4 | 5 |
y | 2 | 3 | 4 | 4 | 5 |
表格1
(1)在给出的坐标系中画出数据x，y的散点图．
(2)补全表格2，根据表格2中的数据和公式
求下列问题．
①求出y关于x的回归直线方程
中的
.
②估计当x＝10时，
的值是多少？
表格2
序号 | x | y | x2 | xy |
1 | 1 | 2 | 1 | 2 |
2 | 2 | 3 | 4 | 6 |
3 | 3 | 4 | 9 | 12 |
4 | 4 | 4 | 16 | 16 |
5 | 5 | 5 | 25 | 25 |
∑ |
