Question

【题目】如图，在平面直角坐标系xOy中，已知椭圆 =1（a＞b＞0）的离心率为 ，长轴长为4，过椭圆的左顶点A作直线l，分别交椭圆和圆x2+y2=a2于相异两点P，Q．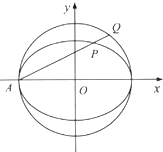

（1）若直线l的斜率为 ，求 的值；
（2）若 =λ ，求实数λ的取值范围．

Answer 1

【答案】
（1）解：由条件可得，2a=4，e= = ，a2﹣b2=c2，

解得a=2，b=c= ，

可得椭圆的方程为 ，圆的方程为x2+y2=4；

（方法一）直线l的方程为 ，由 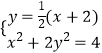得：3x2+4x﹣4=0，

解得 ，所以 ；

所以 ，又因为原点O到直线l的距离 ，

所以 ，

所以 ；

（方法二）由 得3y2﹣4y=0，所以yP= ，

由 可得5y2﹣8y=0，解得yQ= ，

所以 = = × =

（2）解：（方法一）若 ，则λ= ﹣1，

设直线l：y=k（x+2），由 得，（2k2+1）x2+8k2﹣4=0，

即（x+2）[（2k2+1）x+（4k2﹣2）]=0，

所以 ，得 ；

所以 ，

即 ，同理Q（ ， ）， ，

即有λ= ﹣1=1﹣ ，

由k2＞0，可得0＜k2＜1．

（方法二）由方法一可得，λ= ﹣1= ﹣1= ﹣1=1﹣ ，

由题意：k2＞0，所以0＜λ＜1

【解析】（1）由题意可得a=2，运用离心率公式和a，b，c的关系可得b，c，进而得到椭圆方程和圆的方程，设出直线l的方程代入椭圆方程，求得弦长AP，运用圆的弦长公式可AQ，进而所求之比；或联立直线的方程和椭圆方程（或圆的方程）求得P，Q的纵坐标，即可得到所求之比；（2）若 ，则 ，设直线l：y=k（x+2），代入椭圆方程，求得交点，以及弦长AP，代入圆方程可得交点，可得弦长AQ，可得实数λ的式子，运用不等式的性质即可得到所求范围；或将直线方程代入椭圆方程（圆方程）求得P，Q的纵坐标，由坐标之比，结合不等式的性质，即可得到所求范围．