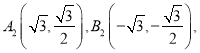Question

【题目】已知全集

（1）若，求实数q的取值范围；

（2）若中有四个元素，求和q的值.

Answer 1

【答案】（1）；

（2）， ={1，3，4，5}

【解析】试题分析：（1）若 =U，则A=，根据一元二次方程根的关系即可求q的取值范围；

（2）若中有四个元素，则等价为A为单元素集合，然后进行求解即可．

试题解析：

（1）∵A=U，

∴A=，即方程x2﹣5qx+4=0无解，或方程x2﹣5qx+4=0的解不在U中．

∴△=25q2﹣16＜0，∴＜q＜，

若方程x2﹣5qx+4=0的解不在U中，

此时满足判别式△=25q2﹣16≥0，即p≥或p≤﹣，

由12﹣5q1+4≠0得q≠1；

由22﹣5q2+4≠0得q≠；

同理，由3、4、5不是方程的根，依次可得q≠，q≠1，q≠；

综上可得所求范围是{q|q∈R，且q≠，q≠1，q≠}．

（2）∵A中有四个元素，∴A为单元素集合，则△=25q2﹣16=0，

即q=±，

当A={1}时，q=1，不满足条件．；

当A={2}时，q=，满足条件．；

当A={3}时，q=，不满足条件．；

当A={4}时，q=1，不满足条件．；

当A={5}时，q=，不满足条件．，

∴q=，此时A={2}，

对应的UA={1，3，4，5}．