题目内容
【题目】(1)已知椭圆方程为![]() ,点
,点![]() .
.
i.若关于原点对称的两点![]() 记直线
记直线![]() 的斜率分别为
的斜率分别为![]() ,试计算
,试计算![]() 的值;
的值;
ii.若关于原点对称的两点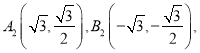 记直线
记直线![]() 的斜率分别为
的斜率分别为![]() ,试计算
,试计算![]() 的值;
的值;
(2)根据上题结论探究:若![]() 是椭圆
是椭圆![]() 上关于原点对称的两点,点
上关于原点对称的两点,点![]() 是椭圆上任意一点,且直线
是椭圆上任意一点,且直线![]() 的斜率都存在,并分别记为
的斜率都存在,并分别记为![]() ,试猜想
,试猜想![]() 的值,并加以证明.
的值,并加以证明.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)i直接求出![]() 、
、![]() 的值,即可得结果;ii直接求出
的值,即可得结果;ii直接求出![]() 的值,即可得结果;(2)根据两种特殊情况进行归纳推理可得:
的值,即可得结果;(2)根据两种特殊情况进行归纳推理可得: ![]() ,其中点
,其中点![]() 是椭圆
是椭圆![]() 上关于原点对称的两点,点
上关于原点对称的两点,点![]() 是椭圆上任意一点,然后设出点
是椭圆上任意一点,然后设出点![]() 的坐标,代入椭圆方程并作差,变形整理即可得到
的坐标,代入椭圆方程并作差,变形整理即可得到![]() 是与点
是与点![]() 位置无关的定值.
位置无关的定值.
试题解析:(1)i. 因为![]() ,
,
所以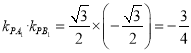
ii. 因为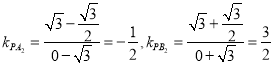 ,
,
所以![]()
(2)猜想![]()
证明: 设点![]() ,则点
,则点![]() ,从而
,从而![]() ,设点
,设点![]() ,
,
由![]() ,
,
得![]() (*)
(*)
由![]() ,
, ![]() ,
,
代入(*)式得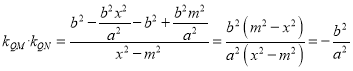
所以![]()

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
【题目】化为推出一款6寸大屏手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如下:
女性用户:
分值区间 |
|
|
|
|
|
频数 | 20 | 40 | 80 | 50 | 10 |
男性用户:
分值区间 |
|
|
|
|
|
频数 | 45 | 75 | 90 | 60 | 30 |
(1)如果评分不低于70分,就表示该用户对手机“认可”,否则就表示“不认可”,完成下列![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为性别对手机的“认可”有关:
的把握认为性别对手机的“认可”有关:
女性用户 | 男性用户 | 合计 | |
“认可”手机 | |||
“不认可”手机 | |||
合计 |
附:
| 0.05 | 0.01 |
| 3.841 | 6.635 |
![]()
(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取2名用户,求2名用户中评分小于90分的概率.