题目内容
【题目】设数列{an}的前n项和为Sn，n∈N*.已知a1＝1，a2＝
，a3＝
，且当n≥2时，4Sn＋2＋5Sn＝8Sn＋1＋Sn－1.
(1)求a4的值；
(2)证明：
为等比数列；
(3)求数列{an}的通项公式．
【答案】见解析
【解析】(1)解：当n＝2时，4S4＋5S2＝8S3＋S1，
即4(a1＋a2＋a3＋a4)＋5(a1＋a2)＝8(a1＋a2＋a3)＋a1，
整理得a4＝
，
又a2＝
，a3＝
，
所以a4＝
.
(2)证明：当n≥2时，有4Sn＋2＋5Sn＝8Sn＋1＋Sn－1，
即4Sn＋2＋4Sn＋Sn＝4Sn＋1＋4Sn＋1＋Sn－1，
∴4(Sn＋2－Sn＋1)＝4(Sn＋1－Sn)－(Sn－Sn－1)，
即an＋2＝an＋1－
an(n≥2)．
经检验，当n＝1时，上式成立．
∵
＝
＝
＝
为常数，且a2－a1＝1，
∴数列
是以1为首项，为公比的等比数列．
(3)解：由(2)知，an＋1－an＝
(n∈N*)，
等式两边同乘2n，
得2nan＋1－2n－1an＝2(n∈N*)．
又20a1＝1，
∴数列{2n－1an}是以1为首项，2为公差的等差数列．
∴2n－1an＝2n－1，
即an＝
(n∈N*)．
则数列{an}的通项公式为an＝ (n∈N*)．
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
【题目】某保险公司有一款保险产品的历史收益率（收益率
利润
保费收入）的频率分布直方图如图所示：
（1）试估计这款保险产品的收益率的平均值；
（2）设每份保单的保费在20元的基础上每增加
元，对应的销量为
（万份）．从历史销售记录中抽样得到如下5组
与
的对应数据：
| 25 | 30 | 38 | 45 | 52 |
销量为 | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
由上表，知
与
有较强的线性相关关系，且据此计算出的回归方程为
．
（ⅰ）求参数
的值；
（ⅱ）若把回归方程
当作
与
的线性关系，用（1）中求出的收益率的平均值作为此产品的收益率，试问每份保单的保费定为多少元时此产品可获得最大利润，并求出最大利润．注：保险产品的保费收入
每份保单的保费
销量．
【题目】某地随着经济的发展，居民收入逐年增长，下表是该地一建设银行连续五年的储蓄存款（年底余额），如下表1：
年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
储蓄存款 | 5 | 6 | 7 | 8 | 10 |
为了研究计算的方便，工作人员将上表的数据进行了处理，
，
得到下表2：
时间代号 | 1 | 2 | 3 | 4 | 5 |
| 0 | 1 | 2 | 3 | 5 |
（Ⅰ）求
关于
的线性回归方程；
（Ⅱ）通过（Ⅰ）中的方程，求出
关于
的回归方程；
（Ⅲ）用所求回归方程预测到2020年年底，该地储蓄存款额可达多少？
（附：对于线性回归方程
）
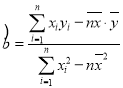
