题目内容
9．已知两圆的方程为x2+y2+6x+8y=0，x2+y2-6x-2y-26=0，判断两圆是否相交，若相交，求过两交点的直线方程及两点间的距离；若不相交，说明理由．分析 通过圆心距与半径的关系确定圆的方程；两圆方程相减得到公共弦的直线方程，再由点到直线的距离公式求公共弦长．
解答 解：由已知圆的方程为x2+y2+6x+8y=0可写为（x+3）2+（y+4）2=25，圆心坐标A（-3，-4），半径为5．
x2+y2-6x-2y-26=0可写为（x-3）2+（y-1）2=36，
∴两圆心之间的距离为：$\sqrt{{（3+3）}^{2}+{（1+4）}^{2}}$=$\sqrt{61}$，满足6-5＜$\sqrt{61}$＜5+6，
即两圆心之间的距离小于两圆半径之和大于两圆半径之差．
∴两圆相交．
⊙A的方程与⊙B的方程左、右两边分别相减得12x+10y+26=0，
即6x+5y+13=0为过两圆交点的直线的方程．
设两交点分别为C、D，则CD：6x+5y+13=0．
点A到直线CD的距离为d=$\frac{|-18-20+13|}{\sqrt{61}}$=$\frac{25}{\sqrt{61}}$．
由勾股定理，得|CD|=2$\sqrt{{5}^{2}-\frac{{25}^{2}}{61}}$=$\frac{60\sqrt{61}}{61}$．
点评 本题考查了两圆位置关系的确定以及点到直线的距离公式的运用；两圆相交时，公共弦所在的直线是两圆方程相减得到的方程．
练习册系列答案
名校课堂系列答案
相关题目
20．
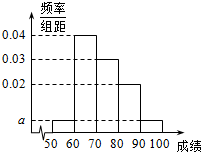某校高二学生有800名，从中抽取100名学生期末考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]
（Ⅰ）求图中α的值；
（Ⅱ）根据频率分布直方图，估计这100名学生语文成绩的平均分、中位数、众数；（精确到个位数）
（Ⅲ）若这100名学生语文成绩某些分数段的人数（x）与数学成绩相应分数段的人数（y）之比如表所示，求推测高二这800名学生中数学成绩在[50，90）之外的人数．
某校高二学生有800名，从中抽取100名学生期末考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]（Ⅰ）求图中α的值；
（Ⅱ）根据频率分布直方图，估计这100名学生语文成绩的平均分、中位数、众数；（精确到个位数）
（Ⅲ）若这100名学生语文成绩某些分数段的人数（x）与数学成绩相应分数段的人数（y）之比如表所示，求推测高二这800名学生中数学成绩在[50，90）之外的人数．
| 分数段 | [50，60） | [60，70） | [70，80） | [80，90） |
| x：y | 1：1 | 2：1 | 3：4 | 4：5 |
17．若函数$f（x）=\left\{\begin{array}{l}1-{2^x}，x≤0\\{x^3}-3x+a，x＞0\end{array}\right.$的值域为[0，+∞），则实数a的取值范围是（ ）
| A． | 3≥a≥2 | B． | 3≥a＞2 | C． | a≤2 | D． | a＜2 |
4．若直线x+（a-1）y+2=0和2x+3y+1=0互相垂直，则a=（ ）
| A． | $\frac{1}{3}$ | B． | -$\frac{2}{3}$ | C． | -$\frac{1}{3}$ | D． | $\frac{2}{3}$ |
1．在平面直角坐标系中，O为坐标原点，P是由不等式组$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{x+y≥1}\end{array}\right.$所确定的平面区域内的动点，点Q是直线3x+4y-7=0上任意一点，O为坐标原点，则|$\overline{OP}+\overline{OQ}$|的最小值为（ ）
| A． | $\frac{7}{5}$ | B． | 2 | C． | $\frac{9}{5}$ | D． | $\frac{11}{5}$ |