题目内容
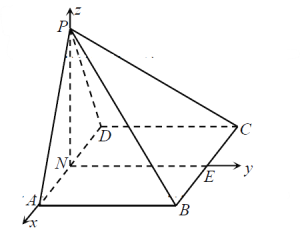
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 的中点.
的中点.
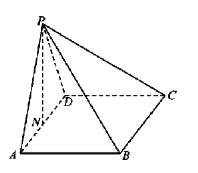
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() ,且
,且![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)由![]() 及矩形可证
及矩形可证![]() 平面
平面![]() ,从而得
,从而得![]() ,再由等腰三角形得一个垂直后可得线面垂直;
,再由等腰三角形得一个垂直后可得线面垂直;
(2)以![]() 为原点,
为原点,![]() 分别为
分别为![]() 轴建立空间直角坐标系(其中
轴建立空间直角坐标系(其中![]() 是
是![]() 中点),写出点的坐标,求出二面角的两个面的法向量,由法向量夹角余弦值得二面角余弦值.
中点),写出点的坐标,求出二面角的两个面的法向量,由法向量夹角余弦值得二面角余弦值.
(1)由题意,知![]() ,
,![]() ,又
,又![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,![]() ,由
,由![]() ,
,![]() 得:
得:![]()
![]() ,
, ![]() 平面
平面![]() ,
,![]() 平面
平面![]()
(2)由![]() ,
,![]() ,
,![]() ,
, ![]() 得:
得:![]()
取![]() 的中点
的中点 ![]() ,连结
,连结![]() ,则
,则![]() ,故
,故![]() ,由(1)知:
,由(1)知:![]() ,
, ![]() ,
, ![]()
以![]() 为原点,
为原点,![]() 分别为
分别为![]() 轴建立空间直角坐标系,于是,有:
轴建立空间直角坐标系,于是,有:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ,
, ![]() ,
,![]()
设平面![]() 的一个法向量为
的一个法向量为![]() ,则由
,则由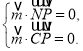 得:
得:![]()
取![]() 得:
得:![]() ,设平面
,设平面![]() 的一个法向量为
的一个法向量为![]()
则由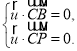 得:
得:![]() ,取
,取![]() 得:
得:![]() ,
,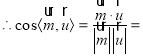
![]()
![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】“绿水青山就是金山银山”,“建设美丽中国”已成为新时代中国特色社会主义生态文明建设的重要内容,某班在一次研学旅行活动中,为了解某苗圃基地的柏树幼苗生长情况,在这些树苗中随机抽取了120株测量高度(单位:![]() ),经统计,树苗的高度均在区间
),经统计,树苗的高度均在区间![]() 内,将其按
内,将其按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
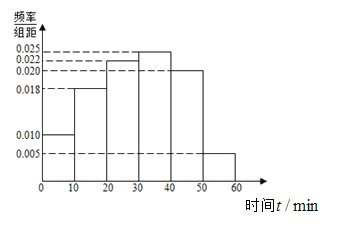
,![]() 分成6组,制成如图所示的频率分布直方图.据当地柏树苗生长规律,高度不低于
分成6组,制成如图所示的频率分布直方图.据当地柏树苗生长规律,高度不低于![]() 的为优质树苗.
的为优质树苗.

(1)求图中![]() 的值;
的值;
(2)已知所抽取的这120株树苗来自于![]() ,
,![]() 两个试验区,部分数据如下列联表:
两个试验区,部分数据如下列联表:
|
| 合计 | |
优质树苗 | 20 | ||
非优质树苗 | 60 | ||
合计 |
将列联表补充完整,并判断是否有99.9%的把握认为优质树苗与![]() ,
,![]() 两个试验区有关系,并说明理由;
两个试验区有关系,并说明理由;
(3)通过用分层抽样方法从![]() 试验区被选中的树苗中抽取5株,若从这5株树苗中随机抽取2株,求优质树苗和非优质树苗各有1株的概率.
试验区被选中的树苗中抽取5株,若从这5株树苗中随机抽取2株,求优质树苗和非优质树苗各有1株的概率.
附:参考公式与参考数据:
其中![]()
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
【题目】在![]() 年俄罗斯索契冬奥会某项目的选拔比赛中,
年俄罗斯索契冬奥会某项目的选拔比赛中,![]() 、
、![]() 两个代表队进行对抗赛,每队三名队员,
两个代表队进行对抗赛,每队三名队员,![]() 队队员是
队队员是![]() 、
、![]() 、
、![]() ,
,![]() 队队员是
队队员是![]() 、
、![]() 、
、![]() ,按以往多次比赛的统计,对阵队员之间胜负概率如下表,现按表中对阵方式出场进行三场比赛,每场胜队得
,按以往多次比赛的统计,对阵队员之间胜负概率如下表,现按表中对阵方式出场进行三场比赛,每场胜队得![]() 分,负队得
分,负队得![]() 分,设
分,设![]() 队、
队、![]() 队最后所得总分分别为
队最后所得总分分别为![]() 、
、![]() 且
且![]() .
.
对阵队员 |
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 队得分为
队得分为![]() 分的概率;
分的概率;
(2)求![]() 的分布列;并用统计学的知识说明哪个队实力较强.
的分布列;并用统计学的知识说明哪个队实力较强.
【题目】某高中为了了解高三学生每天自主参加体育锻炼的情况,随机抽取了100名学生进行调查,其中女生有55名.下面是根据调查结果绘制的学生自主参加体育锻炼时间的频率分布直方图:
将每天自主参加体育锻炼时间不低于40分钟的学生称为体育健康A类学生,已知体育健康A类学生中有10名女生.
(Ⅰ)根据已知条件完成下面![]() 列联表,并据此资料你是否认为达到体育健康A类学生与性别有关?
列联表,并据此资料你是否认为达到体育健康A类学生与性别有关?
非体育健康A类学生 | 体育健康A类学生 | 合计 | |
男生 | |||
女生 | |||
合计 |
(Ⅱ)将每天自主参加体育锻炼时间不低于50分钟的学生称为体育健康![]() 类学生,已知体育健康
类学生,已知体育健康![]() 类学生中有2名女生,若从体育健康
类学生中有2名女生,若从体育健康![]() 类学生中任意选取2人,求至少有1名女生的概率.
类学生中任意选取2人,求至少有1名女生的概率.
附:
P( | 0.05 | 0.010 | 0.005 |
| 3.841 | 6.635 | 7.879 |
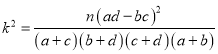
【题目】某市2010年4月1日—4月30日对空气污染指数的监测数据如(主要污染物为可吸入颗粒物):61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,77,86,83,82,82,64,79,86,85,75,71,49,45.
样本频率分布表:
分组 | 频数 | 频率 |
[41,51) | 2 | |
[51,61) | 1 | |
[61,71) | 4 | |
[71,81) | 6 | |
[81,91) | 10 | |
[91,101) | ||
[101,111) | 2 |
(1) 完成频率分布表;
(2)作出频率分布直方图;
(3)根据国家标准,污染指数在0~50之间时,空气质量为优:在51~100之间时,为良;在101~150之间时,为轻微污染;在151~200之间时,为轻度污染.请你依据所给数据和上述标准,对该市的空气质量给出一个简短评价.