题目内容
【题目】下列说法正确的个数是( )
①设某大学的女生体重![]() 与身高
与身高![]() 具有线性相关关系,根据一组样本数据
具有线性相关关系,根据一组样本数据![]() ,用最小二乘法建立的线性回归方程为
,用最小二乘法建立的线性回归方程为![]() ,则若该大学某女生身高增加
,则若该大学某女生身高增加![]() ,则其体重约增加
,则其体重约增加![]() ;
;
②关于![]() 的方程
的方程![]() 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
③过定圆![]() 上一定点
上一定点![]() 作圆的动弦
作圆的动弦![]() ,
,![]() 为原点,若
为原点,若![]() ,则动点
,则动点![]() 的轨迹为椭圆;
的轨迹为椭圆;
④已知![]() 是椭圆
是椭圆![]() 的左焦点,设动点
的左焦点,设动点![]() 在椭圆上,若直线
在椭圆上,若直线![]() 的斜率大于
的斜率大于![]() ,则直线
,则直线![]() (
(![]() 为原点)的斜率的取值范围是
为原点)的斜率的取值范围是![]() .
.
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】
根据回归方程的意义判断①;先推出方程的一根大于1 , 一根大于0小于1,结合椭圆与双曲线离心率定义可判断②;利用参数法求出动点![]() 的轨迹可判断③;由题意画出图形,得到满足直线
的轨迹可判断③;由题意画出图形,得到满足直线![]() 的斜率大于
的斜率大于![]() 的
的![]() 所在的位置,求出直线
所在的位置,求出直线![]() 的斜率的取值范围可判断④.
的斜率的取值范围可判断④.
①根据回归方程的意义,结合回归方程为![]() ,可得该大学某女生身高增加
,可得该大学某女生身高增加![]() ,则其体重约增加
,则其体重约增加![]() ,正确;
,正确;
②关于![]() 的方程
的方程![]() 的两根之和大于2 , 两根之积等于1, 故两根中,一根大于1 , 一根大于0小于1,可分别作为椭圆和双曲线的离心率,正确;
的两根之和大于2 , 两根之积等于1, 故两根中,一根大于1 , 一根大于0小于1,可分别作为椭圆和双曲线的离心率,正确;
③设定圆![]() 的方程为
的方程为![]() ,定点
,定点![]() ,设
,设![]() ,
,![]() ,由
,由![]() ,得
,得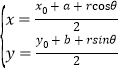 ,消去参数
,消去参数![]() ,得
,得![]() ,即动点
,即动点![]() 的轨迹为圆,③错误.
的轨迹为圆,③错误.
④由![]() ,得
,得![]() ,
,
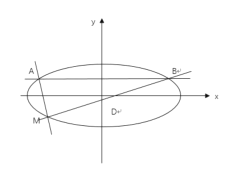
则![]() ,如图:
,如图:
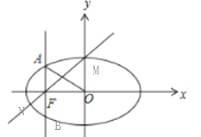
过![]() 作垂直于
作垂直于![]() 轴的直线,交椭圆于
轴的直线,交椭圆于![]() ,过
,过![]() 斜率为
斜率为![]() 的直线与椭圆交于
的直线与椭圆交于![]() ,当
,当![]() 在椭圆弧上
在椭圆弧上![]() 上时,符合题意, 又
上时,符合题意, 又![]() ,
,![]() ,
,![]() ,当
,当![]() 在椭圆弧
在椭圆弧![]() 上时,直线
上时,直线![]() 的斜率的取值范围是
的斜率的取值范围是 ![]() ,当
,当![]() 在椭圆弧
在椭圆弧![]() 上时, 直线
上时, 直线![]() 的斜率的取值范围是
的斜率的取值范围是![]() ,即满足直线
,即满足直线![]() 的斜率大于
的斜率大于![]() ,直线
,直线![]() 的斜率的取值范围是
的斜率的取值范围是![]() 正确,综上可知正确命题个数为3,故选C.
正确,综上可知正确命题个数为3,故选C.

练习册系列答案
相关题目