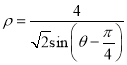Question

【题目】已知函数f（x）= ，设b＞a≥0，若f（a）=f（b），则af（b）的取值范围是（ ）
A.[ ，2）
B.[﹣ ，+∞）
C.[﹣ ，﹣ ）
D.[﹣ ， ]

Answer 1

【答案】A
【解析】解：由函数f（x）= ，作出其图像如图，
因为函数f（x）在[0，1）和[1，+∞）上都是单调函数，
所以，若满足a＞b≥0，时f（a）=f（b），
必有b∈[0，1），a∈[1，+∞），
由图可知，使f（a）=f（b）的b∈[ ，1），
f（a）∈[1，2）．
由不等式的可乘积性得：bf（a）∈[ ，2）．
∴af（b）的取值范围是[ ，2）．
故选：A．
【考点精析】本题主要考查了函数的值的相关知识点，需要掌握函数值的求法：①配方法(二次或四次)；②“判别式法”；③反函数法；④换元法；⑤不等式法；⑥函数的单调性法才能正确解答此题．