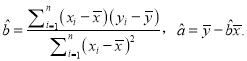Question

【题目】函数f（x）是R上的偶函数，且当x＞0时，函数的解析式为 ．
（1）用定义证明f（x）在（0，+∞）上是减函数；
（2）求当x＜0时，函数的解析式．

Answer 1

【答案】
（1）证明：∵ ，任取x1，x2∈（0，+∞），且x1＜x2；

则f（x1）﹣f（x2）=（ ﹣1）﹣（ ﹣1）= ；

∵0＜x1＜x2，∴x2﹣x1＞0，x1x2＞0；

∴f（x1）﹣f（x2）＞0，即f（x1）＞f（x2）；

∴f（x）在（0，+∞）上是减函数

（2）解：当x＜0时，﹣x＞0，

∵x＞0时， ，

∴f（﹣x）= ﹣1=﹣ ﹣1，

又∵f（x）是R上的偶函数，

∴f（﹣x）=f（x）

∴f（x）=﹣ ﹣1；

即x＜0时，f（x）=﹣ ﹣1

【解析】（1）用函数的单调性定义证明f（x）在（0，+∞）上是减函数；（2）应用偶函数的性质f（﹣x）=f（x），与x＞0时f（x）的解析式，可以求出x＜0时f（x）的解析式．
【考点精析】根据题目的已知条件，利用函数单调性的判断方法的相关知识可以得到问题的答案，需要掌握单调性的判定法：①设x1,x2是所研究区间内任两个自变量，且x1＜x2；②判定f(x1)与f(x2)的大小；③作差比较或作商比较．