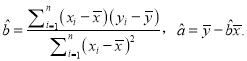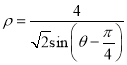题目内容
【题目】在平面直角坐标系![]() 中,过椭圆
中,过椭圆![]() 右焦点的直线
右焦点的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,
两点, ![]() 为
为![]() 的中点,且直线
的中点,且直线![]() 的斜率为
的斜率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设另一直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,原点
两点,原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)由题意,焦点![]() ,所以
,所以![]() ,再由
,再由![]() ,得
,得![]() ,
,
进而得![]() ,即可得到椭圆的标准方程.
,即可得到椭圆的标准方程.
(Ⅱ)由题意,①当直线![]() 的斜率不存在时或者斜率为0时,易得
的斜率不存在时或者斜率为0时,易得![]() ;
;
②设直线![]() 的方程为:
的方程为: ![]() ,由题意,原点
,由题意,原点![]() 到直线
到直线![]() 的距离得到
的距离得到![]() .
.
设交点![]() 的坐标分别为
的坐标分别为![]() ,联立方程组,得到
,联立方程组,得到![]() ,再由弦长公式,利用均值不等式,即可求解最值,进而得到面积的最值.
,再由弦长公式,利用均值不等式,即可求解最值,进而得到面积的最值.
试题解析:
(Ⅰ)由题意,直线![]() 与
与![]() 轴交于焦点:
轴交于焦点: ![]() ,
, ![]() ,设
,设![]() ,
, ![]() ,
, ![]() ,则:
,则: ![]() ,
,
![]() ,
, ![]()
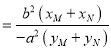
![]() ,
,
![]() ,又
,又![]() ,
, ![]()
![]() ,
,
即椭圆![]() 的方程为:
的方程为: ![]()
(Ⅱ)由题意,①当直线![]() 的斜率不存在时或者斜率为0时,易得
的斜率不存在时或者斜率为0时,易得![]() ;
;
②当直线![]() 的斜率存在时且不为0时,设直线
的斜率存在时且不为0时,设直线![]() 的方程为:
的方程为: ![]() ,由题意,原点
,由题意,原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,故
,故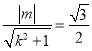 ,
,
![]() .设交点
.设交点![]() 的坐标分别为:
的坐标分别为: ![]() ,
, ![]() ,
,
则: 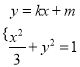 ,
, ![]() ,
,
由题意![]() ,
, ![]()
![]() .
.
![]()
![]()
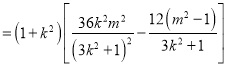
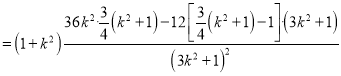
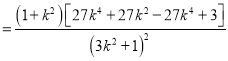
![]()
![]()
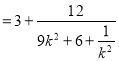
![]() ,
,
当且仅当![]() ,即
,即![]() 时等号成立,
时等号成立, ![]() ;
;
综上所述,当直线![]() 的斜率
的斜率![]() 时,
时,
即![]() 时,
时, ![]() 面积的最大值
面积的最大值
![]()
![]()

【题目】已知函数f(x)=a4x﹣a2x+1+1﹣b(a>0)在区间[1,2]上有最大值9和最小值1
(1)求a,b的值;
(2)若不等式f(x)﹣k4x≥0在x∈[﹣1,1]上有解,求实数k的取值范围.
【题目】某企业为了对生产的一种新产品进行合理定价,将该产品按事先拟定的价格进行试销,得到以下数据:
单价x(元/件) | 60 | 62 | 64 | 66 | 68 | 70 |
销量y(件) | 91 | 84 | 81 | 75 | 70 | 67 |
(I)画出散点图,并求![]() 关于
关于![]() 的回归方程;
的回归方程;
(II)已知该产品的成本是36元/件,预计在今后的销售中,销量与单价仍然服从(I)中的关系,为使企业获得最大利润,该产品的单价应定为多少元(精确到元)?
附:回归直线![]() 的斜率和截距的最小二乘法估计公式分别为:
的斜率和截距的最小二乘法估计公式分别为: