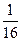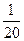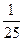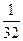题目内容
已知函数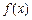 的定义域为R,其导数
的定义域为R,其导数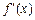 满足0<
满足0<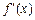 <1.设a是方程
<1.设a是方程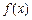 =x的根.
=x的根.
(Ⅰ)当x>a时,求证: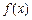 <x;
<x;
(Ⅱ)求证:|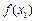 -
-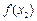 |<|x1-x2|(x1,x2∈R,x1≠x2);
|<|x1-x2|(x1,x2∈R,x1≠x2);
(Ⅲ)试举一个定义域为R的函数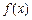 ,满足0<
,满足0<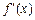 <1,且
<1,且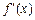 不为常数.
不为常数.
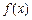 的定义域为R,其导数
的定义域为R,其导数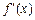 满足0<
满足0<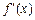 <1.设a是方程
<1.设a是方程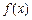 =x的根.
=x的根.(Ⅰ)当x>a时,求证:
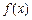 <x;
<x;(Ⅱ)求证:|
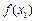 -
-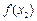 |<|x1-x2|(x1,x2∈R,x1≠x2);
|<|x1-x2|(x1,x2∈R,x1≠x2);(Ⅲ)试举一个定义域为R的函数
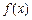 ,满足0<
,满足0<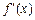 <1,且
<1,且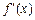 不为常数.
不为常数.同解析
(Ⅰ)令g(x)=f(x) -x,则g`(x)=f `(x) -1<0.故g(x)为减函数,
又因为g(a)=f(a)-a=0,所以当x>a时,g(x)<g(a)=0,
所以f(x) -x<0,即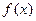 <x. 5分
<x. 5分
(Ⅱ)不妨设x1<x2,由(Ⅰ)知g(x)为减函数,
所以 g(x2)<g(x1),即f(x2)-x2<f(x1)-x1
所以 f(x2)-f(x1)<x2-x1;又因为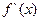 >0,所以
>0,所以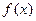 为增函数,
为增函数,
所以0<f(x2)-f(x1)<x2-x1,所以|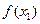 -
-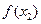 |<|x1-x2|. 11分
|<|x1-x2|. 11分
(Ⅲ)本小题没有统一的答案,满足题设条件的函数有无穷多个.
如f(x)=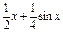 . 16分
. 16分
又因为g(a)=f(a)-a=0,所以当x>a时,g(x)<g(a)=0,
所以f(x) -x<0,即
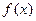 <x. 5分
<x. 5分(Ⅱ)不妨设x1<x2,由(Ⅰ)知g(x)为减函数,
所以 g(x2)<g(x1),即f(x2)-x2<f(x1)-x1
所以 f(x2)-f(x1)<x2-x1;又因为
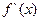 >0,所以
>0,所以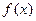 为增函数,
为增函数,所以0<f(x2)-f(x1)<x2-x1,所以|
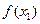 -
-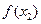 |<|x1-x2|. 11分
|<|x1-x2|. 11分(Ⅲ)本小题没有统一的答案,满足题设条件的函数有无穷多个.
如f(x)=
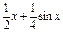 . 16分
. 16分
练习册系列答案
相关题目
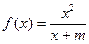 的图像经过点
的图像经过点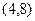 .
.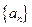 中,若
中,若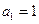 ,
,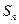 为数列
为数列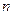 项和,且满足
项和,且满足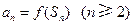 ,
,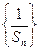 成等差数列,并求数列
成等差数列,并求数列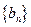 ,若将数列
,若将数列
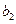
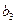
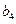
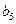
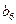
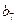
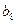
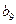
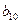
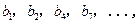 构成的数列即为数列
构成的数列即为数列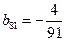 时,求上表中第
时,求上表中第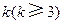 行所有项的和.
行所有项的和.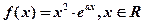 ,其中
,其中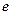 为自然对数的底数,
为自然对数的底数,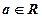 。
。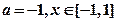 ,求函数
,求函数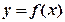 的最值;
的最值;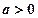 ,都有
,都有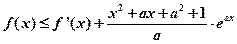 成立,
成立,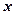 的取值范围。
的取值范围。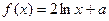 (
(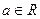 )与函数
)与函数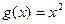 ,
,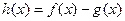 的单调区间;
的单调区间;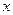 的方程
的方程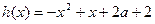 在区间[1,3]内恰有两个相异的实根,求实数
在区间[1,3]内恰有两个相异的实根,求实数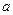 的取值范围.
的取值范围.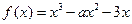
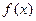 在
在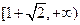 是增函数,导函数
是增函数,导函数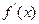 在
在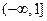 上是减函数,求
上是减函数,求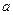 的值;
的值;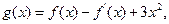 求
求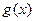 的单调区间.
的单调区间.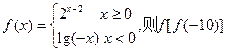 的值为 。
的值为 。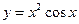 的导数为( )
的导数为( )
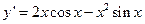
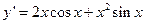

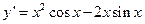
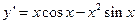
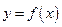 的导函数
的导函数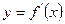 的图像如图所示,则
的图像如图所示,则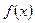 的解析式可能是( )
的解析式可能是( )
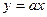
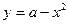
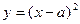
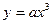
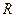 上的函数
上的函数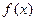 满足
满足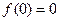 ,
,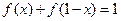 ,
,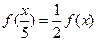 ,且当
,且当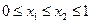 时,有
时,有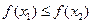 ,则
,则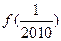 的值为( )
的值为( )