��Ŀ����
���⣨1������2������3������ѡ���⣬ÿС��7�֣��뿼����ѡ2����������14�֣������������������ǰ����Ʒ֣�����ʱ������2BǦ���ڴ���ϰ���ѡ��Ŀ��Ӧ�����Ϳ�ڣ�������ѡ������������У���1��ѡ��4-2��������任
��֪����A=
 ��һ����������ֵ1����������
��һ����������ֵ1���������� ��
������ �����A��
���� ����B=
 ����O��0��0����M��2��-1����N��0��2�������OMN�ھ���AB�Ķ�Ӧ�任���������õ��ġ�O'M'N'�������
����O��0��0����M��2��-1����N��0��2�������OMN�ھ���AB�Ķ�Ӧ�任���������õ��ġ�O'M'N'���������2��ѡ��4-4������ϵ���������
��ֱ֪������ϵxOy�У�ֱ��l�IJ�������Ϊ
 ��tΪ����������ֱ������ϵxOy�е�ԭ��OΪ ���㣬x��ķǸ�����Ϊ���ᣬԲC�ļ����귽��Ϊ��2-4��cos��+3=0��
��tΪ����������ֱ������ϵxOy�е�ԭ��OΪ ���㣬x��ķǸ�����Ϊ���ᣬԲC�ļ����귽��Ϊ��2-4��cos��+3=0������ ��l����ͨ���̼�C��ֱ�����귽�̣�
���� PΪԲC�ϵĵ㣬��P��l�����ȡֵ��Χ��
��3��ѡ��4-5������ʽѡ��
��֪����x�IJ���ʽ��|x-1|+|x+2|��a2+2|a|-5������x��R���������ʵ��a��ȡֵ��Χ��
���𰸡������������ݾ���A= ��һ����������ֵ1����������
��һ����������ֵ1���������� ���ɵ�
���ɵ� ���Ӷ��ɾ���A��
���Ӷ��ɾ���A��
�����ȼ���AB���Ӷ��ɵõ�O��M��N��ɵ�O�䣨0��0����M�䣨4��0����N�䣨0��4�������ɼ����O'M'N'���������2������ֱ��l�IJ���������ȥ�������ɵ���ͨ���̣�ԲC�ļ����귽�����ü�������ֱ������Ļ�����ʽ�ɵ�ֱ�����귽�̣�
����Բ����ͨ����Ϊ�����̣�ȷ��Բ����뾶�������C��l�ľ��룬�Ӷ�����P��l�����ȡֵ��Χ��
��3�����|x-1|+|x+2|����Сֵ���Ӷ�|x-1|+|x+2|��a2+2|a|-5��?x��R��������ȼ���a2+2|a|-5��3���ɴ˿���a��ȡֵ��Χ��
����⣺��1����������֪�� ����
����
��� ����A=
����A= ��
��
����AB=
 =
= ��
��
�� ��
�� ��
�� ��
��
����O��M��N��ɵ�O�䣨0��0����M�䣨4��0����N�䣨0��4������O'M'N'�����Ϊ ×4×4=8��
×4×4=8��
��2������ֱ��l�IJ�������Ϊ ��tΪ����������×
��tΪ����������× -�ڣ��ɵ���ͨ����Ϊ
-�ڣ��ɵ���ͨ����Ϊ =0��
=0��
ԲC�ļ����귽��Ϊ��2-4��cos��+3=0����Ϊֱ�����귽��Ϊx2+y2-4x+3=0������4�֣�
���� C�ı�����Ϊ��x-2��2+y2=1��Բ��C��2��0�����뾶Ϊ1��
��C��l�ľ���Ϊ d= ��
��
��P��l�����ȡֵ��Χ�� ��
��
��3����|x-1|+|x+2|��|��x-1��-��x+2��|=3��
��|x-1|+|x+2|��a2+2|a|-5��?x��R��������ȼ���a2+2|a|-5��3��
����|a|-2����|a|+4����0
��|a|��2��
��a��ȡֵ��Χ��[-2��2]��
���������⿼������������뼫���귽�̡����鲻��ʽ���⣬����Ĺؼ�����ȷ���������չ�ʽ��
 ��һ����������ֵ1����������
��һ����������ֵ1���������� ���ɵ�
���ɵ� ���Ӷ��ɾ���A��
���Ӷ��ɾ���A�������ȼ���AB���Ӷ��ɵõ�O��M��N��ɵ�O�䣨0��0����M�䣨4��0����N�䣨0��4�������ɼ����O'M'N'���������2������ֱ��l�IJ���������ȥ�������ɵ���ͨ���̣�ԲC�ļ����귽�����ü�������ֱ������Ļ�����ʽ�ɵ�ֱ�����귽�̣�
����Բ����ͨ����Ϊ�����̣�ȷ��Բ����뾶�������C��l�ľ��룬�Ӷ�����P��l�����ȡֵ��Χ��
��3�����|x-1|+|x+2|����Сֵ���Ӷ�|x-1|+|x+2|��a2+2|a|-5��?x��R��������ȼ���a2+2|a|-5��3���ɴ˿���a��ȡֵ��Χ��
����⣺��1����������֪��
 ����
����
���
 ����A=
����A= ��
������AB=

 =
= ��
����
 ��
�� ��
�� ��
������O��M��N��ɵ�O�䣨0��0����M�䣨4��0����N�䣨0��4������O'M'N'�����Ϊ
 ×4×4=8��
×4×4=8����2������ֱ��l�IJ�������Ϊ
 ��tΪ����������×
��tΪ����������× -�ڣ��ɵ���ͨ����Ϊ
-�ڣ��ɵ���ͨ����Ϊ =0��
=0��ԲC�ļ����귽��Ϊ��2-4��cos��+3=0����Ϊֱ�����귽��Ϊx2+y2-4x+3=0������4�֣�
���� C�ı�����Ϊ��x-2��2+y2=1��Բ��C��2��0�����뾶Ϊ1��
��C��l�ľ���Ϊ d=
 ��
����P��l�����ȡֵ��Χ��
 ��
����3����|x-1|+|x+2|��|��x-1��-��x+2��|=3��
��|x-1|+|x+2|��a2+2|a|-5��?x��R��������ȼ���a2+2|a|-5��3��
����|a|-2����|a|+4����0
��|a|��2��
��a��ȡֵ��Χ��[-2��2]��
���������⿼������������뼫���귽�̡����鲻��ʽ���⣬����Ĺؼ�����ȷ���������չ�ʽ��

��ϰ��ϵ�д�
�����Ŀ
 ����
���� ����Ӧ�ı任
����Ӧ�ı任 ��ֱ��
��ֱ�� �任Ϊ��������ʵ��
�任Ϊ��������ʵ�� ������
������ �������
������� �IJ������̣�
�IJ������̣� ��
�� Ϊ��������Բ
Ϊ��������Բ �ļ����귽�̣�
�ļ����귽�̣� ��
��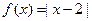
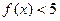 ��
�� ������ʽ
������ʽ ����.
����.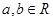 ����
���� ����Ӧ�ı任
����Ӧ�ı任 ��ֱ��
��ֱ�� �任Ϊ��������ʵ��
�任Ϊ��������ʵ�� ������
������ �������
������� �IJ������̣�
�IJ������̣� ��
�� Ϊ��������Բ
Ϊ��������Բ �ļ����귽�̣�
�ļ����귽�̣� ��
��
 ��
�� ������ʽ
������ʽ ����.
����.