题目内容
(本小题满分14分)本题(1)、(2)、(3)三个选答题,每小题7分,任选2题作答,满分14分,如果多做,则按所做的前两题计分。作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中。
(1)(本小题满分7分) 选修4-2:矩阵与变换
已知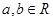 ,若
,若 所对应的变换
所对应的变换 把直线
把直线 变换为自身,求实数
变换为自身,求实数 ,并求
,并求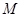 的逆矩阵。
的逆矩阵。
(2)(本题满分7分)选修4-4:坐标系与参数方程
已知直线 的参数方程:
的参数方程: (
( 为参数)和圆
为参数)和圆 的极坐标方程:
的极坐标方程: 。
。
①将直线 的参数方程化为普通方程,圆
的参数方程化为普通方程,圆 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
②判断直线 和圆
和圆 的位置关系。
的位置关系。
(3)(本题满分7分)选修4-5:不等式选讲
已知函数
①解不等式 ;
;
②证明:对任意 ,不等式
,不等式 成立.
成立.
【答案】
(1)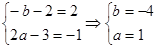 ,
,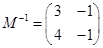
(2)①直线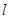 的普通方程为
的普通方程为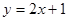 ,⊙
,⊙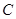 的直角坐标方程为
的直角坐标方程为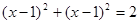
②直线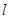 和⊙
和⊙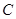 相交。
相交。
(3)①原不等式的解集为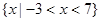
②证明略
【解析】(1) 设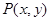 为直线
为直线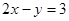 上任意一点其在M的作用下变为
上任意一点其在M的作用下变为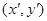
则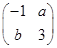
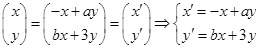
代入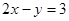 得:
得: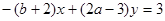 ……………3分
……………3分
其与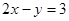 完全一样得
完全一样得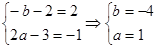
则矩阵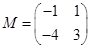 则
则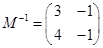 ……………7分
……………7分
(2) 解:①消去参数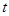 ,得直线
,得直线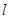 的普通方程为
的普通方程为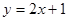 ……………3分
……………3分
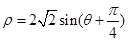 ,即
,即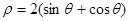 ,
,
两边同乘以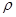 得
得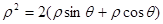 ,
,
得⊙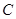 的直角坐标方程为
的直角坐标方程为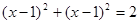 ………5分
………5分
②圆心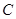 到直线
到直线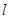 的距离
的距离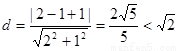 ,所以直线
,所以直线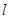 和⊙
和⊙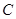 相交…7分
相交…7分
(3)①由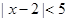 ,解得
,解得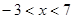
∴原不等式的解集为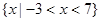 ……………………3分
……………………3分
②证明: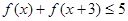 即
即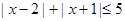
令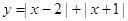 及
及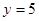 由图得
由图得
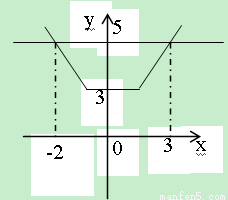
当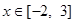 ,不等式成立. ……………………7分
,不等式成立. ……………………7分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)