题目内容
本题(1)、(2)、(3)三个选答题,每小题7分,任选2题作答,满分14分,如果多做,则按所做的前两题计分.(I)选修4-2:矩阵与变换
已知矩阵A=
|
|
(II)选修4-4:坐标系与参数方程
求直线
|
|
(III)选修4-5:不等式选讲
若存在实数x满足不等式|x-4|+|x-3|<a,求实数a的取值范围.
分析:(I)由BA=
=
,得l1变换到l3的变换公式
从而2ax+by+4=0即直线l1:x-y+4=0,列出关于a,b的方程即可求得a,b即可.
(II)先得出直线
的普通方程为x+y+1=0及曲线
即圆心为(1,-1)半径为4的圆 利用圆心(1,-1)到直线的距离即可求得直线被曲线截得的弦长;
(III)先利用绝对值不等式的性质得出y=|x-4|+|x-3|的最小值为1再根据原不等式有实数解,即可求得a的取值范围.
|
|
|
|
(II)先得出直线
|
|
(III)先利用绝对值不等式的性质得出y=|x-4|+|x-3|的最小值为1再根据原不等式有实数解,即可求得a的取值范围.
解答:解:(1)(本小题满分7分)
解:BA=
=
,
得l1变换到l3的变换公式
,…(2分)则2ax+by+4=0即直线l1:x-y+4=0,
则有
解得a=
,b=-1…(4分)
此时B=
,同理可得l2的方程为2y-x+4=0
即x-2y-4=0.…(7分)
(2)(本小题满分7分)
解:直线
的普通方程为x+y+1=0…(2分)
曲线
即圆心为(1,-1)半径为4的圆 …(4分)
则圆心(1,-1)到直线x+y+1=0的距离d=
=
…(5分)
设直线被曲线截得的弦长为t,则t=2
=
,
∴直线被曲线截得的弦长为
…(7分)
(3)(本小题满分7分)
解:∵|x-4|+|x-3|≥|(x-4)-(x-3)|…(2分)∴y=|x-4|+|x-3|的最小值为1 …(4分)
又因为原不等式有实数解,所以a的取值范围是(1,+∞).…(7分)
解:BA=
|
|
|
得l1变换到l3的变换公式
|
则有
|
| 1 |
| 2 |
此时B=
|
即x-2y-4=0.…(7分)
(2)(本小题满分7分)
解:直线
|
曲线
|
则圆心(1,-1)到直线x+y+1=0的距离d=
| |1-1+1| | ||
|
| ||
| 2 |
设直线被曲线截得的弦长为t,则t=2
42-(
|
| 62 |
∴直线被曲线截得的弦长为
| 62 |
(3)(本小题满分7分)
解:∵|x-4|+|x-3|≥|(x-4)-(x-3)|…(2分)∴y=|x-4|+|x-3|的最小值为1 …(4分)
又因为原不等式有实数解,所以a的取值范围是(1,+∞).…(7分)
点评:本小题主要考查几种特殊的矩阵变换、圆的参数方程、不绝对值不等式的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 ,若
,若 所对应的变换
所对应的变换 把直线
把直线 变换为自身,求实数
变换为自身,求实数 ,并求
,并求 的逆矩阵。
的逆矩阵。 的参数方程:
的参数方程: (
( 为参数)和圆
为参数)和圆 的极坐标方程:
的极坐标方程: 。
。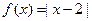
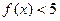 ;
; ,不等式
,不等式 成立.
成立.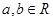 ,若
,若 所对应的变换
所对应的变换 把直线
把直线 变换为自身,求实数
变换为自身,求实数 ,并求
,并求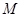 的逆矩阵。
的逆矩阵。 的参数方程:
的参数方程: (
( 为参数)和圆
为参数)和圆 的极坐标方程:
的极坐标方程: 。
。
 ;
; ,不等式
,不等式 成立.
成立.