题目内容
(2012•漳州模拟)本题(1)、(2)、(3)三个选答题,每小题7分,请考生任选2题作答,满分14分,如果多做,则按所做的前两题计分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中.
(1)选修4-2:矩阵与变换
已知矩阵A=
有一个属于特征值1的特征向量
=
.
(Ⅰ) 求矩阵A;
(Ⅱ) 矩阵B=
,点O(0,0),M(2,-1),N(0,2),求△OMN在矩阵AB的对应变换作用下所得到的△O'M'N'的面积.
(2)选修4-4:坐标系与参数方程
已知直角坐标系xOy中,直线l的参数方程为
(t为参数).以直角坐标系xOy中的原点O为 极点,x轴的非负半轴为极轴,圆C的极坐标方程为ρ2-4ρcosθ+3=0,
(Ⅰ) 求l的普通方程及C的直角坐标方程;
(Ⅱ) P为圆C上的点,求P到l距离的取值范围.
(3)选修4-5:不等式选讲
已知关于x的不等式:|x-1|+|x+2|≥a2+2|a|-5对任意x∈R恒成立,求实数a的取值范围.
(1)选修4-2:矩阵与变换
已知矩阵A=
|
| α |
|
(Ⅰ) 求矩阵A;
(Ⅱ) 矩阵B=
|
(2)选修4-4:坐标系与参数方程
已知直角坐标系xOy中,直线l的参数方程为
|
(Ⅰ) 求l的普通方程及C的直角坐标方程;
(Ⅱ) P为圆C上的点,求P到l距离的取值范围.
(3)选修4-5:不等式选讲
已知关于x的不等式:|x-1|+|x+2|≥a2+2|a|-5对任意x∈R恒成立,求实数a的取值范围.
分析:(Ⅰ)根据矩阵A=
有一个属于特征值1的特征向量
=
,可得
=1•
,从而可矩阵A;
(Ⅱ)先计算AB,从而可得点O,M,N变成点O′(0,0),M′(4,0),N′(0,4),即可计算△O'M'N'的面积;(2)(Ⅰ)直线l的参数方程消去参数,可得普通方程,圆C的极坐标方程利用极坐标与直角坐标的互化公式可得直角坐标方程;
(Ⅱ)化圆的普通方程为标准方程,确定圆心与半径,求出点C到l的距离,从而可求P到l距离的取值范围;
(3)求出|x-1|+|x+2|的最小值,从而|x-1|+|x+2|≥a2+2|a|-5对?x∈R恒成立,等价于a2+2|a|-5≤3,由此可求a的取值范围.
|
| α |
|
|
|
|
(Ⅱ)先计算AB,从而可得点O,M,N变成点O′(0,0),M′(4,0),N′(0,4),即可计算△O'M'N'的面积;(2)(Ⅰ)直线l的参数方程消去参数,可得普通方程,圆C的极坐标方程利用极坐标与直角坐标的互化公式可得直角坐标方程;
(Ⅱ)化圆的普通方程为标准方程,确定圆心与半径,求出点C到l的距离,从而可求P到l距离的取值范围;
(3)求出|x-1|+|x+2|的最小值,从而|x-1|+|x+2|≥a2+2|a|-5对?x∈R恒成立,等价于a2+2|a|-5≤3,由此可求a的取值范围.
解答:解:(1)(Ⅰ)由已知得
=1•
,∴
解得
,故A=
.
(Ⅱ)AB=
=
,
∴(AB)
=
=
,(AB)
=
=
,(AB)
=
=
,
即点O,M,N变成点O′(0,0),M′(4,0),N′(0,4),△O'M'N'的面积为
×4×4=8.
(2)(Ⅰ)直线l的参数方程为
(t为参数),①×
-②,可得普通方程为
x-y+3
=0,
圆C的极坐标方程为ρ2-4ρcosθ+3=0,化为直角坐标方程为x2+y2-4x+3=0.…(4分)
(Ⅱ) C的标准方程为(x-2)2+y2=1,圆心C(2,0),半径为1,
点C到l的距离为 d=
=
,
∴P到l距离的取值范围是[
-1 ,
+1].
(3)∵|x-1|+|x+2|≥|(x-1)-(x+2)|=3,
∴|x-1|+|x+2|≥a2+2|a|-5对?x∈R恒成立,等价于a2+2|a|-5≤3,
即(|a|-2)(|a|+4)≤0
∴|a|≤2,
∴a的取值范围是[-2,2].
|
|
|
|
解得
|
|
(Ⅱ)AB=
|
|
|
∴(AB)
|
|
|
|
|
|
|
|
|
|
|
|
即点O,M,N变成点O′(0,0),M′(4,0),N′(0,4),△O'M'N'的面积为
| 1 |
| 2 |
(2)(Ⅰ)直线l的参数方程为
|
| 3 |
| 3 |
| 3 |
圆C的极坐标方程为ρ2-4ρcosθ+3=0,化为直角坐标方程为x2+y2-4x+3=0.…(4分)
(Ⅱ) C的标准方程为(x-2)2+y2=1,圆心C(2,0),半径为1,
点C到l的距离为 d=
2
| ||||
| 2 |
5
| ||
| 2 |
∴P到l距离的取值范围是[
5
| ||
| 2 |
5
| ||
| 2 |
(3)∵|x-1|+|x+2|≥|(x-1)-(x+2)|=3,
∴|x-1|+|x+2|≥a2+2|a|-5对?x∈R恒成立,等价于a2+2|a|-5≤3,
即(|a|-2)(|a|+4)≤0
∴|a|≤2,
∴a的取值范围是[-2,2].
点评:本题考查矩阵、参数方程与极坐标方程、考查不等式问题,解题的关键是明确方法、掌握公式.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
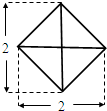 (2012•漳州模拟)一个几何体的正视图、侧视图、俯视图都是如图所示正方形及其对角线,则该几何体的体积等于( )
(2012•漳州模拟)一个几何体的正视图、侧视图、俯视图都是如图所示正方形及其对角线,则该几何体的体积等于( ) (2012•漳州模拟)如图是某社区工会对当地企业工人月收入情况进行一次抽样调查后画出的频率分布直方图,其中第二组月收入在[1.5,2)千元的频数为300,则此次抽样的样本容量为( )
(2012•漳州模拟)如图是某社区工会对当地企业工人月收入情况进行一次抽样调查后画出的频率分布直方图,其中第二组月收入在[1.5,2)千元的频数为300,则此次抽样的样本容量为( )