题目内容
已知三条直线l1:2x-y+a=0(a>0),l2:-4x+2y+1=0和l3:x+y-1=0,且l1与l2的距离是
;
(1)求a的值;
(2)能否找到一点P同时满足下列三个条件:
①P是第一象限的点;
②点P到l1的距离是点P到l2的距离的
;
③点P到l1的距离与点P到l3的距离之比是
:
?若能,求点P的坐标;若不能,请说明理由.
7
| ||
| 10 |
(1)求a的值;
(2)能否找到一点P同时满足下列三个条件:
①P是第一象限的点;
②点P到l1的距离是点P到l2的距离的
| 1 |
| 2 |
③点P到l1的距离与点P到l3的距离之比是
| 2 |
| 5 |
(1)∵直线l1:-4x+2y-2a=0(a>0),l2:-4x+2y+1=0,且l1与l2的距离是
,
∴
=
,解得 a=3.
(2)设点P的坐标为(m,n),m>0,n>0,
若P点满足条件②,则点P在与l1、l2平行的直线l′:2x-y+C=0上,∴
=
•
,
解得 C=
,或C=
,故有 2m-n+
=0,或2m-n+
=0.
若P点满足条件③,由题意及点到直线的距离公式可得,
=
,化简可得|2m-n+3|=|m+n-1|,故有2m-n+3=m+n-1 或2m-n+3=-(m+n-1).
即 m-2n+4=0,或3m+2=0(舍去).
联立 2m-n+
=0 和 m-2n+4=0解得
,应舍去.
联立2m-n+
=0和 m-2n+4=0解得
,
故点P的坐标为(
,
),故能找到一点P同时满足这三个条件.
7
| ||
| 10 |
∴
| |-2a-1| | ||
|
7
| ||
| 10 |
(2)设点P的坐标为(m,n),m>0,n>0,
若P点满足条件②,则点P在与l1、l2平行的直线l′:2x-y+C=0上,∴
| |C-3| | ||
|
| 1 |
| 2 |
|C+
| ||
|
解得 C=
| 13 |
| 2 |
| 11 |
| 6 |
| 13 |
| 2 |
| 11 |
| 6 |
若P点满足条件③,由题意及点到直线的距离公式可得,
| ||||
|
| ||
|
即 m-2n+4=0,或3m+2=0(舍去).
联立 2m-n+
| 13 |
| 2 |
|
联立2m-n+
| 11 |
| 6 |
|
故点P的坐标为(
| 1 |
| 9 |
| 37 |
| 18 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的直径
的直径 的长为4,点
的长为4,点 平分弧
平分弧 ,过
,过 ,交
,交 .
. :
: 的角平分线,求
的角平分线,求 的长.
的长.
 ,则它的边与半径为
,则它的边与半径为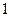 的圆的公共点个数最多为( )
的圆的公共点个数最多为( )



 (a>0,b>0)与y轴的交点关于原点的对称点称为“望点”,以“望点”为圆心,凡是与曲线C有公共点的圆,皆称之为“望圆”,则当a=1,b=1时,所有的“望圆”中,面积最小的“望圆”的面积为________.
(a>0,b>0)与y轴的交点关于原点的对称点称为“望点”,以“望点”为圆心,凡是与曲线C有公共点的圆,皆称之为“望圆”,则当a=1,b=1时,所有的“望圆”中,面积最小的“望圆”的面积为________.