题目内容
点P是曲线x2-y-1nx=0上的任意一点,则点P到直线y=x-2的最小距离______.
点P是曲线y=x2-lnx上任意一点,当过点P的切线和直线y=x-2平行时,
点P到直线y=x-2的距离最小.
由于直线y=x-2的斜率等于1,令y=x2-lnx的导数 y′=2x-
=1,x=1,或 x=-
(舍去),
故曲线y=x2-lnx上和直线y=x-2平行的切线经过的切点坐标(1,1),
点(1,1)到直线y=x-2的距离等于
,故点P到直线y=x-2的最小距离为
,
故答案为:
.
点P到直线y=x-2的距离最小.
由于直线y=x-2的斜率等于1,令y=x2-lnx的导数 y′=2x-
| 1 |
| x |
| 1 |
| 2 |
故曲线y=x2-lnx上和直线y=x-2平行的切线经过的切点坐标(1,1),
点(1,1)到直线y=x-2的距离等于
| 2 |
| 2 |
故答案为:
| 2 |

练习册系列答案
相关题目
 =0与圆
=0与圆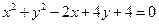 没有公共点,则实数m的取值范围是 .
没有公共点,则实数m的取值范围是 .
 上,圆C过坐标原点O,且与x轴、y轴交于A、B两点,则△OAB的面积是( )
上,圆C过坐标原点O,且与x轴、y轴交于A、B两点,则△OAB的面积是( )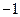 )为圆心且与直线
)为圆心且与直线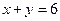 相切的圆
相切的圆 的方程是 .
的方程是 .