题目内容

5．设点P（x，y）在椭圆4x2+y2=4上，则x+y的最大值为$\sqrt{5}$，最小值为$-\sqrt{5}$．

分析 由题意方程求得椭圆的参数方程，然后利用三角函数最值的求法得答案．

解答 解：由椭圆4x2+y2=4，得${x}^{2}+\frac{{y}^{2}}{4}=1$，
可设椭圆参数方程为$\left\{\begin{array}{l}{x=cosθ}\\{y=2sinθ}\end{array}\right.$，
∴x+y=2sinθ+cosθ=$\sqrt{5}（\frac{2\sqrt{5}}{5}sinθ+\frac{\sqrt{5}}{5}cosθ）$
=$\sqrt{5}sin（θ+φ）$（tanφ=$\frac{1}{2}$）．
∴x+y的最大值为$\sqrt{5}$，x+y的最小值为-$\sqrt{5}$．
故答案为：$\sqrt{5}$，$-\sqrt{5}$．

点评 本题考查椭圆的简单几何性质，考查了椭圆参数方程的应用，训练了三角函数的最值的求法，是中档题．

练习册系列答案
相关题目
15．已知平面上一定点C（2，O）和直线l：x=8，P为该平面上一动点，作PQ⊥l，垂足为Q，且（$\overrightarrow{PC}$+$\frac{1}{2}$$\overrightarrow{PQ}$）•（$\overrightarrow{PC}$-$\frac{1}{2}$$\overrightarrow{PQ}$）=0．
（1）求动点P的轨迹方程；
（2）若EF为圆N：x2+（y-1）2=1的任一条直径，求$\overrightarrow{PE}$•$\overrightarrow{PF}$的最小值．
16．若a＞0，且a≠1，设函数f（x）=$\left\{\begin{array}{l}{{a}^{|x|}，x＜1}\\{|{x}^{2}-2x|，x≥1}\end{array}\right.$，若不等式f（x）≤3的解集是（-∞，3]，则a的取值范围是（　　）
A．（1，+∞）B．（1，3）C．（0，1）D．[3，+∞）
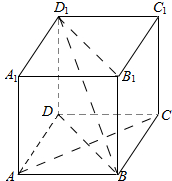13．如图，ABCD-A1B1C1D1是棱长为a的正方体．求证：
（1）D${\;}_{{1}_{\;}}$B⊥AC；
（2）BC1⊥平面A1B1CD．
20．（1）已知f（$\frac{2}{x}$+1）=lgx，求f（x）；
（2）已知f（x）是一次函数，且满足3f（x+1）-2f（x-1）=2x+17，求f（x）；
（3）定义在（-1，1）内的函数f（x）满足2f（x）-f（-x）=lg（x+1），求函数f（x）的解析式．
10．已知函数y=f（x）的定义域为R，且不恒为0，且对任意x，y∈R，都有f（x+y）=f（x）+f（y）．
（1）求f（0）的值；
（2）判断函数y=f（x）的奇偶性；
（3）当x＞0时，f（x）＜0，判断函数y=f（x）的单调性．
17．已知关于x的不等式组$\left\{\begin{array}{l}{（2x-3）（3x+2）≤0}\\{x-a＞0}\end{array}\right.$无实数解，求实数a的取值范围．
14．已知函数f（x）=x2-2ax+2（a∈R）．
（1）若函数f（x）在（-∞，2）上单调递减，求实数a的取值范围；
（2）求函数f（x）在[-1，2]上的值域．
15．已知函数f（x）=$\left\{\begin{array}{l}{2，x∉[-2，2]}\\{|x|，x∈[-2，2]}\end{array}\right.$，则其最小值为（　　）
A．2B．0C．-2D．不存在

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网