题目内容
15.已知函数f(x)=$\left\{\begin{array}{l}{2,x∉[-2,2]}\\{|x|,x∈[-2,2]}\end{array}\right.$,则其最小值为( )| A. | 2 | B. | 0 | C. | -2 | D. | 不存在 |
分析 对f(x)的各段分别求范围,可得f(x)的值域为[0,2],即可得到最小值.
解答 解:由分段函数可得,当x∉[-2,2]时,f(x)=2;
当x∈[-2,2]时,f(x)=|x|∈[0,2].
即有f(x)的最小值为0.
故答案为:B.
点评 本题考查分段函数的最值的求法,注意求各段的范围再求并集,考查运算能力,属于基础题.

练习册系列答案
相关题目
7.在等差数列{an}中,Sp=q,Sq=q,Sp+q的值为( )
| A. | p+q | B. | -(p+q) | C. | p2-q2 | D. | p2+q2 |
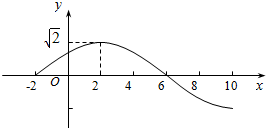 已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<$\frac{π}{2}$)的部分图象如图所示.