题目内容
6.二次函数f(x)=ax2+bx+c,f(x)=0的两根是1和3,且f(f(x))=0有唯一实根.①求f(x)的解析式;
②求|f(x)|在区间[t,t+1]上的最大值;
③设②中的最大值为M(t),若k≤M(t)对任意实数t恒成立,求k的取值范围.
分析 ①f(x)=a(x-1)(x-3),f(f(x))=0有唯一实根,可得f(x)=1或f(x)=3为函数的极值点,即可求出求f(x)的解析式;
②分类讨论,即可求出|f(x)|在区间[t,t+1]上的最大值;
③设②中的最大值为M(t),求出M(t)的最小值,即可求k的取值范围.
解答 解:①f(x)=ax2+bx+c,f(x)=0的两根是1和3,则1+3=-$\frac{b}{a}$,1×3=$\frac{c}{a}$,
∴b=-4a,c=3a,
∴f(x)=a(x-1)(x-3),
f(f(x))=0有唯一实根,可得f(x)=1或f(x)=3为函数的极值点,
a>0,则f(x)min=3,∴f(2)=-a=3,∴a=-3,矛盾;
a<0,则f(x)min=1,∴f(2)=-a=1,∴a=-1,
∴f(x)的解析式为f(x)=-(x-1)(x-3);
②|f(x)|=$\left\{\begin{array}{l}{{x}^{2}-4x+3,x<1或x>3}\\{-{x}^{2}+4x-3,1≤x≤3}\end{array}\right.$
在区间[t,t+1]上的最大值=$\left\{\begin{array}{l}{{t}^{2}-4t+3,t≤\frac{3-\sqrt{3}}{2}}\\{-{t}^{2}+2t,\frac{3-\sqrt{3}}{2}<t<1}\\{1,1≤t≤2}\\{-{t}^{2}+4t-3,2<t<\frac{3+\sqrt{3}}{2}}\\{{t}^{2}-2t,t≥\frac{3+\sqrt{3}}{2}}\end{array}\right.$;
③②中的最大值为M(t)的最小值为$\frac{\sqrt{3}}{2}$,若k≤M(t)对任意实数t恒成立,k的取值范围是(-∞,$\frac{\sqrt{3}}{2}$].
点评 本题考查函数的零点,解析式的确定,考查函数的最大值,考查恒成立问题,考查学生分析解决问题的能力,属于中档题.

(1)求a与b的值;
(2)求满足f(x)>0的x的集合A.
| A. | (5,-7) | B. | (2,-1) | C. | (8,-1) | D. | (2,6) |
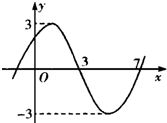
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{12}$ |
| A. | 18 | B. | 9 | C. | 12 | D. | 11 |