题目内容
1．函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，φ∈[0，2π））的图象如图所示，则φ的值为（ ）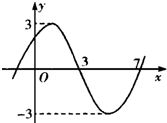
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{12}$ |
分析 根据三角函数的图象确定A，ω和φ的值即可得到结论．
解答 解：由图象知A=3，函数的周期T=2×（7-3）=2×4=8，
即$\frac{2π}{ω}$=8，则ω=$\frac{2π}{8}$=$\frac{π}{4}$，
即f（x）=3sin（$\frac{π}{4}$x+φ），
由五点对应法得当x=3时，$\frac{π}{4}$×3+φ=π，
解得φ=$\frac{π}{4}$，
故选：B．
点评 本题主要考查三角函数解析式的求解，利用图象得到A，ω和φ的值是解决本题的关键．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
2．已知数列{an}是递减数列，且an=（m2-2m）•（n3-2n），则实数m的取值范围为（ ）
| A． | 0＜m＜2 | B． | 0＜m＜$\sqrt{2}$ | C． | -$\sqrt{2}$＜m＜$\sqrt{2}$ | D． | -$\sqrt{2}$＜m＜0 |
13．已知x＞0，y＞0，则下列表达式正确的是（ ）
| A． | x${\;}^{co{s}^{2}θ}$y${\;}^{si{n}^{2}θ}$＜$\sqrt{2{x}^{2}+2{y}^{2}}$＜x+y | |
| B． | x${\;}^{co{s}^{2}θ}$y${\;}^{si{n}^{2}θ}$＜x+y≤$\sqrt{2{x}^{2}+2{y}^{2}}$ | |
| C． | x+y＜x${\;}^{co{s}^{2}θ}$y${\;}^{si{n}^{2}θ}$＜$\sqrt{2{x}^{2}+2{y}^{2}}$ | |
| D． | x+y≤$\sqrt{2{x}^{2}+2{y}^{2}}$＜x${\;}^{co{s}^{2}θ}$y${\;}^{si{n}^{2}θ}$ |