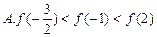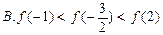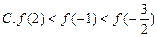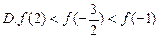题目内容
(10分)已知函数 .
.
(1)求实数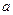 的范围,使
的范围,使 在区间
在区间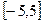 上是单调函数。 (2)求
上是单调函数。 (2)求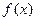 的最小值。
的最小值。
 .
.(1)求实数
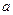 的范围,使
的范围,使 在区间
在区间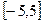 上是单调函数。 (2)求
上是单调函数。 (2)求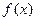 的最小值。
的最小值。(1)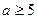 或
或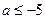 .
.
(2)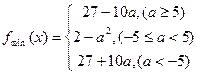
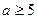 或
或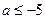 .
.(2)
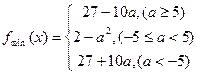
解:(1)因为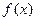 是开口向上的二次函数,且对称轴为
是开口向上的二次函数,且对称轴为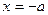 ,为了使
,为了使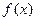 在
在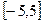 上是单调函数,故
上是单调函数,故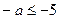 或
或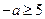 ,即
,即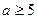 或
或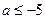 . (4分)
. (4分)
(2)当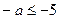 ,即
,即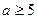 时,
时,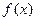 在
在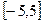 上是增函数,
上是增函数,
所以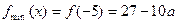 (6分)
(6分)
当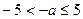 ,即
,即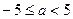 时,
时,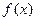 在
在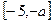 上是减函数,在
上是减函数,在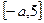 上是增函数,所以
上是增函数,所以 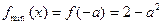 (8分)
(8分)
当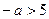 ,即
,即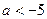 时,
时,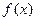 在
在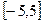 上是减函数,所以
上是减函数,所以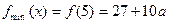
综上可得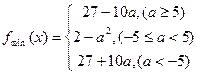 (10分)
(10分)
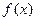 是开口向上的二次函数,且对称轴为
是开口向上的二次函数,且对称轴为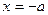 ,为了使
,为了使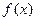 在
在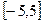 上是单调函数,故
上是单调函数,故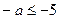 或
或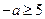 ,即
,即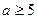 或
或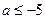 . (4分)
. (4分)(2)当
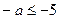 ,即
,即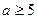 时,
时,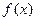 在
在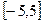 上是增函数,
上是增函数,所以
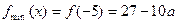 (6分)
(6分)当
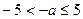 ,即
,即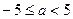 时,
时,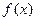 在
在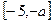 上是减函数,在
上是减函数,在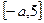 上是增函数,所以
上是增函数,所以 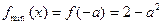 (8分)
(8分)当
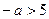 ,即
,即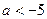 时,
时,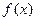 在
在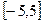 上是减函数,所以
上是减函数,所以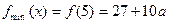
综上可得
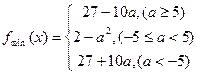 (10分)
(10分)
练习册系列答案
相关题目
 是定义在
是定义在 的增函数,且
的增函数,且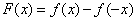 ,那么
,那么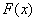 一定是( )
一定是( ) ,有下列四个命题:
,有下列四个命题: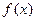 是奇函数; ②
是奇函数; ②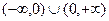 ;
;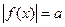 总有四个不同的解;④
总有四个不同的解;④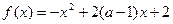 在
在 上是增函数,则实数
上是增函数,则实数 的范围是
的范围是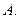
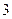
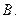
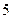 C.
C.
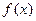 ,满足
,满足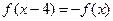 ,且在区间[0,2]上是增函数,则 ( )
,且在区间[0,2]上是增函数,则 ( ) 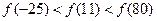
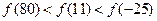

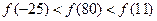
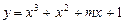 是
是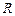 上的单调函数,则实数
上的单调函数,则实数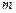 的取值范围是 ( )
的取值范围是 ( )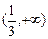
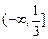
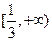
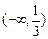
 在区间
在区间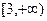 上为单调增函数,则
上为单调增函数,则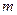 的取值范围为( )
的取值范围为( )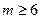


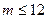
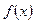 在
在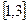 上为增函数,且有最小值0,则它在
上为增函数,且有最小值0,则它在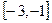 上( )
上( )
 总有
总有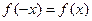 ,且
,且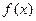 在区间
在区间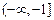 上是增函数,则 ( )
上是增函数,则 ( )