题目内容
已知函数f(x)=ax2-(a+2)x+lnx.
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)当a>0时,若f(x)在区间[1,e]上的最小值为-2,求a的取值范围.
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)当a>0时,若f(x)在区间[1,e]上的最小值为-2,求a的取值范围.
(1)y=-2 (2)[1,+∞)
解:(1)当a=1时,f(x)=x2-3x+lnx,f′(x)=2x-3+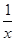 .
.
因为f′(1)=0,f(1)=-2,
所以切线方程是y=-2.
(2)函数f(x)=ax2-(a+2)x+lnx的定义域是(0,+∞).
当a>0时,f′(x)=2ax-(a+2)+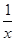 =
=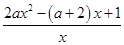 (x>0).
(x>0).
令f′(x)=0,即f′(x)=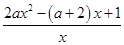 =
=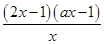 =0,
=0,
得x=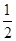 或x=
或x=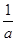 .
.
当0<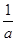 ≤1,即a≥1时,f(x)在[1,e]上单调递增,
≤1,即a≥1时,f(x)在[1,e]上单调递增,
所以f(x)在[1,e]上的最小值是f(1)=-2;
当1<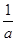 <e时,f(x)在[1,e]上的最小值f(
<e时,f(x)在[1,e]上的最小值f(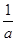 )<f(1)=-2,不合题意;
)<f(1)=-2,不合题意;
当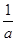 ≥e时,f(x)在[1,e]上单调递减.
≥e时,f(x)在[1,e]上单调递减.
所以f(x)在[1,e]上的最小值f(e)<f(1)=-2,不合题意.
综上a的取值范围为[1,+∞).
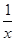 .
.因为f′(1)=0,f(1)=-2,
所以切线方程是y=-2.
(2)函数f(x)=ax2-(a+2)x+lnx的定义域是(0,+∞).
当a>0时,f′(x)=2ax-(a+2)+
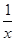 =
=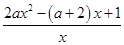 (x>0).
(x>0).令f′(x)=0,即f′(x)=
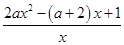 =
=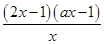 =0,
=0,得x=
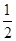 或x=
或x=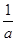 .
.当0<
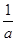 ≤1,即a≥1时,f(x)在[1,e]上单调递增,
≤1,即a≥1时,f(x)在[1,e]上单调递增,所以f(x)在[1,e]上的最小值是f(1)=-2;
当1<
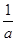 <e时,f(x)在[1,e]上的最小值f(
<e时,f(x)在[1,e]上的最小值f(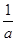 )<f(1)=-2,不合题意;
)<f(1)=-2,不合题意;当
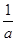 ≥e时,f(x)在[1,e]上单调递减.
≥e时,f(x)在[1,e]上单调递减.所以f(x)在[1,e]上的最小值f(e)<f(1)=-2,不合题意.
综上a的取值范围为[1,+∞).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 .
. 的单调区间和极值;
的单调区间和极值;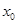 ,使得
,使得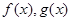 在
在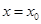 的切线相同?若存在,求出
的切线相同?若存在,求出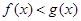 在
在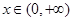 恒成立,求
恒成立,求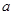 的取值范围.
的取值范围.
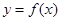 是定义在R上的可导函数,则下列说法不正确的是( )
是定义在R上的可导函数,则下列说法不正确的是( )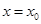 时取得极值,则
时取得极值,则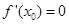
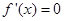 ,则
,则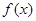 在
在 ,和抛物线相切且与直线
,和抛物线相切且与直线 平行的的直线方程为 ( )
平行的的直线方程为 ( )
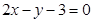


 -x2+1(0<x<2)的图象上任意点处切线的倾斜角记为α,则α的最小值是( )
-x2+1(0<x<2)的图象上任意点处切线的倾斜角记为α,则α的最小值是( )



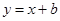 是曲线
是曲线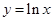 的一条切线,则实数
的一条切线,则实数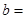 __________.
__________.