题目内容
）设（2-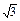
x）100=a0+a1x+a2x2+…+a100x100，求下列各式的值：
（1）a0;
(2)a1+a2+…+a100;
(3)a1+a3+a5+…+a99;
(4)(a0+a2+…+a100)2-(a1+a3+…+a99)2.
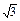x）100=a0+a1x+a2x2+…+a100x100，求下列各式的值：（1）a0;
(2)a1+a2+…+a100;
(3)a1+a3+a5+…+a99;
(4)(a0+a2+…+a100)2-(a1+a3+…+a99)2.
(1) 2100 (2)(2-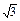)100-2100 (3)
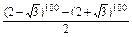（4）1
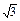)100-2100 (3) 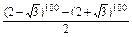（4）1（1）由（2-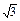x)100展开式中的常数项为C
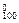·2100,
即a0=2100，或令x=0，则展开式可化为a0=2100.
（2）令x=1,可得
a0+a1+a2+…+a100=(2-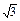)100. ①
∴a1+a2+…+a100=(2-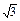)100-2100.
(3)令x=-1可得
a0-a1+a2-a3+…+a100=(2+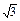)100. ②
与x=1所得到的①联立相减可得，
a1+a3+…+a99=.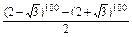
(4)原式=［（a0+a2+…+a100）+(a1+a3+…+a99)］×［(a0+a2+…+a100)-(a1+a3+…+a99)］
=(a0+a1+a2+…+a100)(a0-a1+a2-a3+…+a98-a99+a100)
=(2-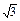)100·（2+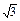）100="1."
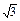x)100展开式中的常数项为C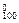·2100,即a0=2100，或令x=0，则展开式可化为a0=2100.
（2）令x=1,可得
a0+a1+a2+…+a100=(2-
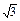)100. ①∴a1+a2+…+a100=(2-
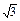)100-2100.(3)令x=-1可得
a0-a1+a2-a3+…+a100=(2+
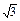)100. ②与x=1所得到的①联立相减可得，
a1+a3+…+a99=
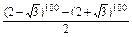.(4)原式=［（a0+a2+…+a100）+(a1+a3+…+a99)］×［(a0+a2+…+a100)-(a1+a3+…+a99)］
=(a0+a1+a2+…+a100)(a0-a1+a2-a3+…+a98-a99+a100)
=(2-
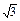)100·（2+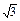）100="1." 
练习册系列答案
相关题目
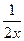)n的展开式中前三项的系数成等差数列，则展开式中x4项的系数为
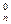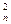＋C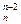
＋…＋C
＋C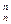
＝（ ）。
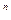
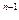
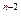
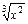+3x2）n展开式中各项的系数和比各项的二项式系数和大992.求展开式中系数最大的项.
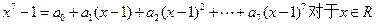恒成立，则
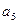值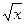
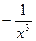）n的展开式中第二项与第三项的系数之和等于27，则n等于 ，系数最大的项是第 项。
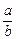的范围.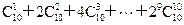
的值为_______ ．
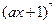的展开式中，
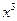的系数是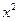
的系数与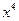
的系数的等差中项，若实数
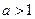，则
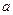的值为 ．