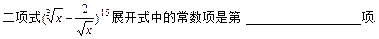题目内容
(12分)在二项式(axm+bxn)12(a>0,b>0,m、n≠0)中有2m+n=0,如果它的展开式里最大系数项恰是常数项. (1)求它是第几项(2)求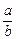 的范围.
的范围.
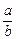 的范围.
的范围.(1)5 (2)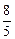 ≤
≤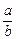 ≤
≤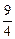
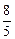 ≤
≤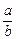 ≤
≤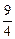
(1)设T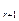 =C
=C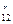 (axm)12-r·(bxn)r=C
(axm)12-r·(bxn)r=C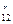 a12-rbrxm(12-r)+nr为常数项,
a12-rbrxm(12-r)+nr为常数项,
则有m(12-r) +nr=0,即m(12-r)-2mr=0,∴r=4,它是第5项.
+nr=0,即m(12-r)-2mr=0,∴r=4,它是第5项.
(2)∵第5项又是系数最大的项,
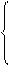 C
C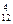 a8b4≥C
a8b4≥C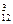 a9b3,①C
a9b3,①C
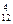 a8b4≥C
a8b4≥C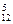 a7b5. ②由①得
a7b5. ②由①得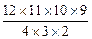 a8b4≥
a8b4≥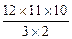 a9b3,
a9b3,
∵a>0,b>0,∴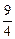 b≥a,即
b≥a,即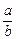 ≤
≤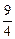 .由②得
.由②得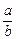 ≥
≥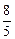 ,∴
,∴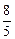 ≤
≤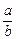 ≤
≤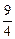 .
.
合要求的不同种法有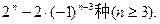
 ………14分
………14分
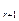 =C
=C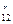 (axm)12-r·(bxn)r=C
(axm)12-r·(bxn)r=C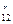 a12-rbrxm(12-r)+nr为常数项,
a12-rbrxm(12-r)+nr为常数项,则有m(12-r)
 +nr=0,即m(12-r)-2mr=0,∴r=4,它是第5项.
+nr=0,即m(12-r)-2mr=0,∴r=4,它是第5项.(2)∵第5项又是系数最大的项,
|
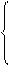 C
C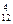 a8b4≥C
a8b4≥C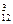 a9b3,①C
a9b3,①C
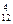 a8b4≥C
a8b4≥C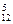 a7b5. ②由①得
a7b5. ②由①得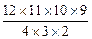 a8b4≥
a8b4≥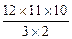 a9b3,
a9b3,∵a>0,b>0,∴
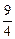 b≥a,即
b≥a,即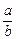 ≤
≤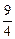 .由②得
.由②得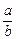 ≥
≥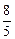 ,∴
,∴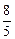 ≤
≤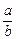 ≤
≤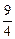 .
.合要求的不同种法有
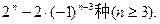
 ………14分
………14分
练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
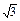 x)100=a0+a1x+a2x2+…+a100x100,求下列各式的值:
x)100=a0+a1x+a2x2+…+a100x100,求下列各式的值: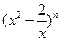 展开式的二项式系数之和比
展开式的二项式系数之和比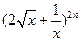 展开式的二项式系数之和小
展开式的二项式系数之和小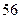 .
. ;
;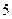 项.
项.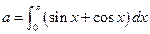 ,则二项式
,则二项式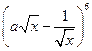 展开式中含
展开式中含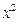 项的系数
项的系数
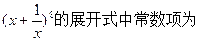
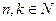 且
且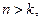 若
若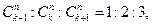 则
则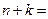 ______.
______.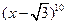 的展开式中,
的展开式中,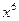 的系数是 .
的系数是 .