题目内容
【题目】如图，在正方形ABCD－A1B1C1D1中，E，F，M分别是棱B1C1，BB1，C1D1的中点，是否存在过点E，M且与平面A1FC平行的平面？若存在，请作出并证明；若不存在，请说明理由.
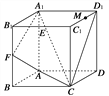
【答案】详见解析.
【解析】试题分析: 由正方体的特征及N为BB1的中点，可知平面A1FC与直线DD1相交，且交点为DD1的中点G.若过M，E的平面α与平面A1FCG平行，注意到EM∥B1D1∥FG，则平面α必与CC1相交于点N，结合M，E为棱C1D1，B1C1的中点，易知C1N∶C1C＝
.于是平面EMN满足要求．
试题解析:
如图，设N是棱C1C上的一点，且C1N＝
C1C时，平面EMN过点E，M且与平面A1FC平行．
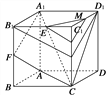
证明如下：设H为棱C1C的中点，连接B1H，D1H.
∵C1N＝C1C，
∴C1N＝
C1H.
又E为B1C1的中点，
∴EN∥B1H.
又CF∥B1H，
∴EN∥CF.
又EN平面A1FC，CF平面A1FC，
∴EN∥平面A1FC.
同理MN∥D1H，D1H∥A1F，
∴MN∥A1F.
又MN平面A1FC，A1F平面A1FC，
∴MN∥平面A1FC.
又EN∩MN＝N，
∴平面EMN∥平面A1FC.
点睛:本题考查线面平行的判定定理和面面平行的判定定理的综合应用,属于中档题.直线和平面平行的判定定理:平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行; 平面与平面平行的判定定理：一个平面内的两条相交直线与另一个平面分别平行，则这两个平面平行．
阅读快车系列答案
【题目】（本小题满分12分，第（1）问 6 分，第（2）问 6 分）
某品牌新款夏装即将上市，为了对夏装进行合理定价，在该地区的三家连锁店各进行了两天试销售，得到如下数据：
连锁店 | A店 | B店 | C店 | |||
售价 | 80 | 86 | 82 | 88 | 84 | 90 |
销售量 | 88 | 78 | 85 | 75 | 82 | 66 |
（1）以三家连锁店分别的平均售价和平均销量为散点，求出售价与销量的回归直线方程
；
（2）在大量投入市场后，销售量与单价仍然服从（1）中的关系，且该夏装成本价为40元/件，为使该款夏装在销售上获得最大利润，该款夏装的单价应定为多少元（保留整数）？
【题目】电视连续剧《人民的名义》自2017年3月28日在湖南卫视开播以来，引发各方关注，收视率、点击率均占据各大排行榜首位．我们用简单随机抽样的方法对这部电视剧的观看情况进行抽样调查，共调查了600人，得到结果如下：其中图1是非常喜欢《人民的名义》这部电视剧的观众年龄的频率分布直方图；表1是不同年龄段的观众选择不同观看方式的人数．
观看方式 年龄（岁） | 电视 | 网络 |
| 150 | 250 |
| 120 | 80 |
求：（I）假设同一组中的每个数据用该组区间的中点值代替，求非常喜欢《人民的名义》这部电视剧的观众的平均年龄；
（II）根据表1，通过计算说明我们是否有99%的把握认为观看该剧的方式与年龄有关？
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附： 
